2904. Ладейная атака

На шахматной доске вырезано несколько клеток, координаты которых задаются. Вам следует так разместить наибольшее количество ладей на шахматной доске, чтобы они не атаковали друг друга. Ладья атакует те клетки шахматной доски, которые находятся в одной с ней горизонтали или вертикали. Ладьи нельзя размещать на вырезанных квадратах. Вырезанные квадраты не являются преградой для атаки ладей.

Вход. Состоит из нескольких тестов. Первая строка каждого теста содержит три целых числа: ширина rows и длина cols (1 ≤ rows, cols ≤ 300) доски в клетках, а также количество вырезанных клеток cuts. Следующая строка содержит список (x, y) координат вырезанных клеток, разделенных пробелом. Список имеет вид x₁ y₁ x₂ y₂ x₃ y₃ ... x_cuts y_cuts. Известно, что 0 ≤ x_i ≤ rows – 1, 0 ≤ y_i ≤ cols – 1.

Выход. Для каждого теста выведите в отдельной строке наибольшее количество ладей, которое можно расположить на доске так, чтобы они не били друг друга.

Пример входа	Пример выхода
8 8 0 3 3 6 0 0 1 0 1 1 2 0 2 1 2 2 3 3 3 0 0 1 2 2 2	8 2 3

РЕШЕНИЕ

графы - потоки

Анализ алгоритма

Построим двудольный граф. В первую долю поместим rows вершин, во вторую – cols вершин. Если клетка с координатами (i, j) останется не вырезанной на шахматной доске, то проведем ребро между i - ой вершиной первой доли и j - ой вершиной второй доли. Максимальное паросочетание полученного двудольного графа равно максимальному количеству неатакующих ладей, которое можно разместить на шахматной доске. Задачу решаем при помощи максимального потока, добавив две вершины: исток и сток.

Например, для третьего теста шахматная доска и построенный граф будут иметь вид:

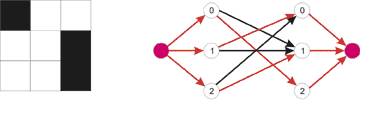
Красным цветом выделены насыщенные ребра в максимальном потоке. Величина потока равна 3, ладьи располагаются в клетках (0, 2), (1, 0) и (2, 1).

При построении матрицы пропускных способностей m вершины графа имеют следующие номера:

· исток: номер 0;

· первая доля: от 1 до rows;

· вторая доля: от rows + 1 до rows + cols;

· сток: номер rows + cols + 1;

Пример

В третьем тесте вырезаны клетки (0, 0), (1, 2), (2, 2). На доске можно расположить 3 ладьи, которые не бьют друг друга.

Реализация алгоритма

Объявим глобальные массивы и переменные.

#define MAX 602

int m[MAX][MAX], used[MAX], MaxFlow, flow;

Функция aug находит дополняющий путь из x в t поиском в глубину и возвращает величину максимального потока в нем.

int aug(int x,int t,int CurFlow)

{

if (x == t) return CurFlow;

if (used[x]++) return 0;

for (int Flow,y = 0; y < n; y++)

{

if (m[x][y] > 0 && (Flow = aug(y,t,min(CurFlow,m[x][y]))))

{

m[x][y] -= Flow; m[y][x] += Flow;

return Flow;

}

}

return 0;

}

Функция BuildMatrix строит двудольный граф в матрице смежности m как описано в анализе алгоритма.

void BuildMatrix(void)

{

int i, j, a, b;

Обнуляем матрицу смежности m. Переменная n содержит количество вершин графа.

memset(m,0,sizeof(m));

n = rows + cols + 2;

for(i = 1; i <= rows; i++) m[0][i] = 1;

for(i = 1; i <= cols; i++) m[i+rows][n-1] = 1;

Заполняем граф, считая, что дырок на доске нет. Проводим ребро между каждой вершиной первой и второй доли.

for(i = 1; i <= rows; i++)

for(j = 1; j <= cols; j++) m[i][j+rows] = 1;

Для каждой дырки с координатами (a, b) удаляем ребро между вершиной a первой доли и вершиной b второй доли.

for(i = 0; i < cuts; i++)

{

scanf("%d %d",&a,&b);

m[a+1][rows+b+1] = 0;

}

}

Основная часть программы. Читаем входные данные. Строим матрицу и запускаем алгоритм поиска максимального потока.

while(scanf("%d %d %d",&rows,&cols,&cuts) == 3)

{

BuildMatrix();

MaxFlow = 0;

do

{

memset(used,0,sizeof(used));

} while ((flow = aug(0,n-1,0x7FFFFFFF)) && (MaxFlow += flow));

printf("%d\n",MaxFlow);

}

Реализация при помощи дополняющего пути с оптимизацией

#include <cstdio>

#include <vector>

#include <algorithm>

#define MAX 301

using namespace std;

int g[MAX][MAX];

vector<int> used, par, mt;

int i, j, ptr;

int rows, cols, cuts, a, b, flow;

int dfs(int v)

{

if (used[v]) return 0;

used[v] = 1;

for (int to = 0; to < cols; to++)

{

if (g[v][to] == 0) continue;

if (mt[to] == -1 || dfs(mt[to]))

{

mt[to] = v;

par[v] = 1;

return 1;

}

}

return 0;

}

void AugmentingPath(void)

{

int i, run;

mt.assign (cols, -1);

par.assign (rows, -1);

for (run = 1; run; )

{

run = 0; used.assign(rows, 0);

for (i = 0; i < rows; i++)

if ((par[i] == -1) && dfs(i)) run = 1;

}

}

int main(void)

{

while(scanf("%d %d %d",&rows,&cols,&cuts) == 3)

{

for(i = 0; i < rows; i++)

for(j = 0; j < cols; j++) g[i][j] = 1;

for(i = 0; i < cuts; i++)

{

scanf("%d %d",&a,&b);

g[a][b] = 0;

}

AugmentingPath();

for (flow = i = 0; i < cols; i++)

if (mt[i] != -1) flow++;

printf("%d\n",flow);

}

return 0;

}