2905.
Переключение света
Фермер Джон
пытается приучить коров к остроумию, позволяя им играть с интеллектуальными
игрушками. Одной из таких игрушек являются лампочки в сарае. Над каждым из n (2 ≤ n ≤ 100,000) коровьих стойл, последовательно пронумерованных
от 1 до n, находится лампочка.
Сначала все
лампочки выключены. Коровы контролируют свет набором из n кнопочных переключателей, которые изменяют состояние лампочек;
нажатие кнопки i изменяет состояние i-ой лампочки с “выкл” на “вкл” или с “вкл” на “выкл”.
Коровы выполняют
набор из m (1 ≤ m ≤ 100,000) команд, каждая из
которых описывается одним из двух целых чисел (0 ≤ команда ≤ 1).
В первом типе
команды (обозначается 0) задаются два целых числа Si и Ei
(1 ≤ Si ≤ Ei ≤ n), описывающих начальный и конечный переключатель.
Выполнение команды состоит в том, что коровы нажимают все переключатели от Si до Ei в точности по одному разу.
Во втором типе
команды (обозначается 1) требуется подсчитать количество включенных ламп в
интервале от Si до Ei (1 ≤ Si ≤ Ei ≤ n) включительно.
Помогите Фермеру
Джону проверить правильность выполнения команд коровами.
Вход. Первая строка содержит два целых числа n и m.
Каждая из следующих m строк содержит
команду, которая описывается тремя целыми числами команда, Si и Ei.
Выход. Для каждого запроса второго типа следует вывести ответ на
него в отдельной строке.
|
Пример
входа |
Пример
выхода |
|
4 5 0 1 2 0 2 4 1 2 3 0 2 4 1 1 4 |
1 2 |
РЕШЕНИЕ
структуры данных – дерево отрезков
Анализ алгоритма
Для решения
задачи следует реализовать дерево отрезков, поддерживающее групповую
модификацию – операцию исключающего ИЛИ (XOR) и суммирование.
В каждом узле
дерева будут поддерживаться значения двух переменных: суммы на отрезке summa и некоторого дополнительного
значения add. Равенство add единице означает, что значения всех элементов соответствующего отрезка следует
изменить на противоположное.
Протолкнуть
значение add по дереву на один
уровень ниже означает пересчитать значения summa
левого и правого поддерева, а также изменить значения add левого и правого поддерева на противоположное (0 на 1, или 1 на
0), тем самым рекурсивно обеспечив проталкивание значения add до листьев дерева.
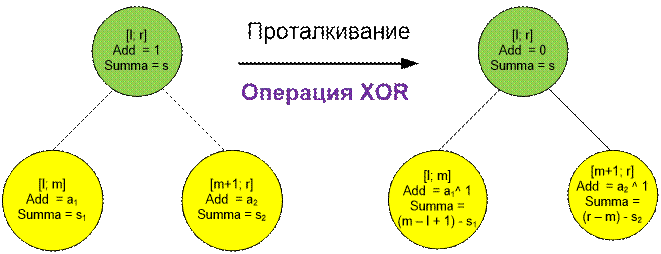
Операцию
проталкивания следует производить не только при выполнении операции прибавления
на отрезке, но и при вычислении сумм.
Пусть отрезок [a; b]
соответствует некоторой вершине дерева, и значения всех его элементов следует изменить на противоположное. Тогда
количество включенных лампочек summa
станет равно числу выключенных до этого лампочек b – a + 1 – summa.
Реализация алгоритма
Дерево отрезков храним в векторе SegTree структур node.
#define MAX 100000
struct node
{
int summa, add;
};
vector<node> SegTree;
Функция Push производит проталкивание значения add вершины v в сыновья. Если add ≠ 0, то следует провести изменение состояния переключателей во всех
элементах левого и правого поддерева. После проталкивания значение add в
вершине v ставим равным 0.
void Push(int v, int lpos, int mid, int rpos)
{
if
(SegTree[v].add == 0) return;
SegTree[2*v].add
^= SegTree[v].add;
SegTree[2*v].summa
= (mid - lpos + 1) - SegTree[2*v].summa;
SegTree[2*v+1].add
^= SegTree[v].add;
SegTree[2*v+1].summa
= (rpos - mid) - SegTree[2*v+1].summa;
SegTree[v].add
= 0;
}
Функция SwitchValue
меняет значения всех элементов отрезка [left; right] на противоположное (включает или
выключает свет).
Вершине v соответствует отрезок [lpos; rpos].
void SwitchValue(int v, int lpos, int rpos, int left, int right)
{
if (left >
right) return;
Если [left; right] соответствует отрезку, который
хранится в вершине дерева [lpos; rpos], то в текущей вершине дерева увеличиваем значение add на единицу по модулю два, а
количество включенных лампочек summa
на отрезке становится равным числу выключенных до этого на этом же отрезке ламп.
if ((lpos == left)
&& (rpos == right))
{
SegTree[v].add
= 1 - SegTree[v].add;
SegTree[v].summa
= (right - left + 1) - SegTree[v].summa;
return;
}
Находим середину отрезка mid = (lpos + rpos)
/ 2.
int mid
= (lpos + rpos) / 2;
Проведем проталкивание, если add не равно нулю.
Push(v, lpos, mid, rpos);
Рекурсивно обрабатываем левого и правого сына текущей вершины
дерева отрезков.
SwitchValue(2*v, lpos,
mid, left, min(mid, right));
SwitchValue(2*v+1,
mid+1, rpos, max(left, mid+1), right);
Пересчитываем значение суммы в вершине v через значения сумм ее детей.
SegTree[v].summa
= SegTree[2*v].summa + SegTree[2*v+1].summa;
}
Функция Summa
возвращает значение суммы на отрезке [left; right].
Вершине v соответствует отрезок [lpos; rpos].
int Summa(int v, int lpos, int rpos, int left, int right)
{
if (left > right) return 0;
Если [left; right] совпадает с отрезком [lpos; rpos], который хранится в вершине v дерева,
то возвращаем находящееся в ней значение суммы.
if ((lpos == left) && (rpos == right))
return SegTree[v].summa;
Находим середину отрезка mid = (lpos + rpos)
/ 2.
int mid = (lpos + rpos) / 2;
Проведем проталкивание, если add не равно нулю.
Push(v, lpos, mid, rpos);
Разбиваем отрезок [lpos; rpos] на [lpos; mid] и [mid + 1; rpos]. Запускаем рекурсивно вычисление сумм на подотрезках.
Складываем полученные суммы.
return Summa(2*v, lpos, mid, left, min(mid, right)) +
Summa(2*v+1, mid+1, rpos, max(left, mid+1), right);
}
Основная часть программы. Читаем
входные данные. Все элементы дерева отрезков изначально содержат нули. Поэтому
строить его нет необходимости.
scanf("%d
%d",&n,&m);
SegTree.resize(4*n);
Последовательно обрабатываем m запросов.
for(i = 0; i < m; i++)
{
scanf("%d %d %d",&type,&Left,&Right);
if (type == 1)
printf("%d\n",Summa(1,1,n,Left,Right));
else
SwitchValue(1,1,n,Left,Right);
}