2905. Light
Switching
Farmer John tries to keep
the cows sharp by letting them play with intellectual toys. One of the larger
toys is the lights in the barn. Each of the n
(2 ≤ n ≤ 100,000) cow
stalls conveniently numbered from 1 to n
has a colorful light above it.
At the beginning of the
evening, all the lights are off. The cows control the lights with a set of n pushbutton switches that toggle the
lights; pushing switch i changes the
state of light i from off to on or
from on to off.
The cows read and execute
a list of m (1 ≤ m ≤ 100,000) operations expressed
as one of two integers (0 ≤ operation
≤ 1).
The first kind of
operation (denoted by a 0 command) includes two subsequent integers Si and Ei (1 ≤ Si
≤ Ei ≤ n) that indicate a starting switch and
ending switch. They execute the operation by pushing each pushbutton from Si through Ei inclusive exactly once.
The second kind of
operation (denoted by a 1 command) asks the cows to count how many lights are
on in the range given by two integers Si
and Ei (1 ≤ Si ≤ Ei ≤ n) which specify the inclusive range in
which the cows should count the number of lights that are on.
Help Farmer John ensure
the cows are getting the correct answer by processing the list and producing
the proper counts.
Input. The first line contains two space-separated integers n and m. Each of the next m
lines represents an operation with three space-separated integers: operation, Si and Ei.
Output. For each operation of the second kind print the answer as an
integer on a single line.
|
Sample
input |
Sample output |
|
4 5 0 1 2 0 2 4 1 2 3 0 2 4 1 1 4 |
1 2 |
SOLUTION
data structures – segment tree
Algorithm analysis
Для решения
задачи следует реализовать дерево отрезков, поддерживающее групповую
модификацию – операцию исключающего ИЛИ (XOR) и суммирование.
В каждом узле
дерева будут поддерживаться значения двух переменных: суммы на отрезке summa и некоторого дополнительного
значения add. Равенство add единице означает, что значения всех элементов соответствующего отрезка следует
изменить на противоположное.
Протолкнуть
значение add по дереву на один
уровень ниже означает пересчитать значения summa
левого и правого поддерева, а также изменить значения add левого и правого поддерева на противоположное (0 на 1, или 1 на
0), тем самым рекурсивно обеспечив проталкивание значения add до листьев дерева.
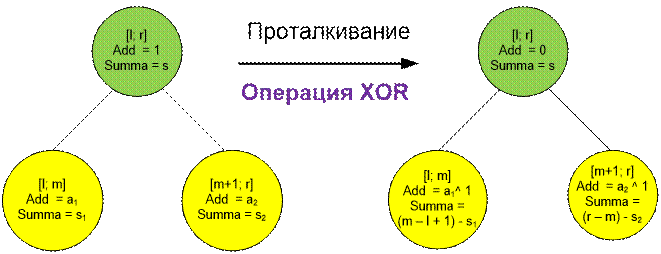
Операцию
проталкивания следует производить не только при выполнении операции прибавления
на отрезке, но и при вычислении сумм.
Пусть отрезок [a; b]
соответствует некоторой вершине дерева, и значения всех его элементов следует изменить на противоположное. Тогда
количество включенных лампочек summa
станет равно числу выключенных до этого лампочек b – a + 1 – summa.
Реализация алгоритма
Дерево отрезков храним в векторе SegTree структур node.
#define MAX 100000
struct node
{
int summa, add;
};
vector<node> SegTree;
Функция Push производит проталкивание значения add вершины v в сыновья. Если add ≠ 0, то следует провести изменение состояния переключателей во всех
элементах левого и правого поддерева. После проталкивания значение add в
вершине v ставим равным 0.
void Push(int v, int lpos, int mid, int rpos)
{
if
(SegTree[v].add == 0) return;
SegTree[2*v].add
^= SegTree[v].add;
SegTree[2*v].summa
= (mid - lpos + 1) - SegTree[2*v].summa;
SegTree[2*v+1].add
^= SegTree[v].add;
SegTree[2*v+1].summa
= (rpos - mid) - SegTree[2*v+1].summa;
SegTree[v].add
= 0;
}
Функция SwitchValue
меняет значения всех элементов отрезка [left; right] на противоположное (включает или
выключает свет).
Вершине v соответствует отрезок [lpos; rpos].
void SwitchValue(int v, int lpos, int rpos, int left, int right)
{
if (left >
right) return;
Если [left; right] соответствует отрезку, который
хранится в вершине дерева [lpos; rpos], то в текущей вершине дерева увеличиваем значение add на единицу по модулю два, а
количество включенных лампочек summa
на отрезке становится равным числу выключенных до этого на этом же отрезке ламп.
if ((lpos == left)
&& (rpos == right))
{
SegTree[v].add
= 1 - SegTree[v].add;
SegTree[v].summa
= (right - left + 1) - SegTree[v].summa;
return;
}
Находим середину отрезка mid = (lpos + rpos)
/ 2.
int mid
= (lpos + rpos) / 2;
Проведем проталкивание, если add не равно нулю.
Push(v, lpos, mid, rpos);
Рекурсивно обрабатываем левого и правого сына текущей вершины
дерева отрезков.
SwitchValue(2*v, lpos,
mid, left, min(mid, right));
SwitchValue(2*v+1,
mid+1, rpos, max(left, mid+1), right);
Пересчитываем значение суммы в вершине v через значения сумм ее детей.
SegTree[v].summa
= SegTree[2*v].summa + SegTree[2*v+1].summa;
}
Функция Summa
возвращает значение суммы на отрезке [left; right].
Вершине v соответствует отрезок [lpos; rpos].
int Summa(int v, int lpos, int rpos, int left, int right)
{
if (left > right) return 0;
Если [left; right] совпадает с отрезком [lpos; rpos], который хранится в вершине v дерева,
то возвращаем находящееся в ней значение суммы.
if ((lpos == left) && (rpos == right))
return SegTree[v].summa;
Находим середину отрезка mid = (lpos + rpos)
/ 2.
int mid = (lpos + rpos) / 2;
Проведем проталкивание, если add не равно нулю.
Push(v, lpos, mid, rpos);
Разбиваем отрезок [lpos; rpos] на [lpos; mid] и [mid + 1; rpos]. Запускаем рекурсивно вычисление сумм на подотрезках.
Складываем полученные суммы.
return Summa(2*v, lpos, mid, left, min(mid, right)) +
Summa(2*v+1, mid+1, rpos, max(left, mid+1), right);
}
Основная часть программы. Читаем
входные данные. Все элементы дерева отрезков изначально содержат нули. Поэтому
строить его нет необходимости.
scanf("%d
%d",&n,&m);
SegTree.resize(4*n);
Последовательно обрабатываем m запросов.
for(i = 0; i < m; i++)
{
scanf("%d %d %d",&type,&Left,&Right);
if (type == 1)
printf("%d\n",Summa(1,1,n,Left,Right));
else
SwitchValue(1,1,n,Left,Right);
}