2923. Дерево

Задано подвешенное дерево, содержащее n (1 ≤ n ≤ 10⁶) вершин. Каждая вершина покрашена в один из n цветов. Требуется для каждой вершины v вычислить количество различных цветов, встречающихся в поддереве с корнем v.

Вход. В первой строке задано число n. Следующие n строк описывают вершины по одной в строке. Описание очередной вершины i имеет вид p_i c_i, где p_i – номер родителя вершины i, а c_i – цвет вершины i (1 ≤ c_i ≤ n). Для корня дерева p_i = 0.

Выход. Выведите n чисел, обозначающих количества различных цветов в поддеревьях с корнями в вершинах 1, 2, ..., n.

Пример входа	Пример выхода
5 2 1 3 2 0 3 3 3 2 1	1 2 3 1 1

РЕШЕНИЕ

поиск в глубину

Анализ алгоритма

Запустим поиск в глубину из корня дерева. Для каждой вершины i храним множество s_i, в котором будем накапливать цвета вершин в ее поддеревьях. Если j – сын вершины i при поиске в глубину, то s_j должно включаться в s_i. Количество различных цветов в поддереве с корнем i равно размеру множества s_i.

Пример

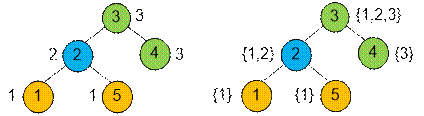
Слева возле каждой вершины приведен ее цвет. Справа возле каждой вершины приведено множество цветов в поддереве с корнем в этой вершине.

Реализация алгоритма

В ячейке color[i] храним цвет i-ой вершины. Во множестве s[i] будем накапливать цвета в поддереве с корнем i. Ориентированное дерево храним в списке смежности графа g. В res[i] храним количество различных цветов в поддереве с корнем i.

#define MAX 1000010

int color[MAX], res[MAX];

set<int> s[MAX];

vector<vector<int> > g;

Функция dfs совершает поиск в глубину из вершины v. Изначально заносим в s[v] цвет вершины v. Для каждого ребра дерева (v, to) добавляем множество s[to] в s[v]. Количество различных цветов в поддереве с корнем v равно размеру множества s[v], заносим его в res[v].

void dfs(int v)

{

int i, to;

s[v].insert(color[v]);

for(i = 0; i < g[v].size(); i++)

{

to = g[v][i];

dfs(to);

Если размер множества s[v] меньше размера множества s[to], то меняем их местами. Далее содержимое меньшего множества s[to] добавляем во множество s[v].

if (s[v].size() < s[to].size()) s[v].swap(s[to]);

s[v].insert(s[to].begin(), s[to].end());

Очищаем множество s[to] – оно нам больше не пригодится.

s[to].clear();

}

res[v] = s[v].size();

}

Основная часть программы. Читаем входные данные.

scanf("%d",&n);

g.resize(n+1);

for(i = 1; i <= n; i++)

{

scanf("%d %d",&p,&c);

g[p].push_back(i);

color[i] = c;

}

Запускаем поиск в глубину из корня дерева – нулевой вершины.

dfs(0);

Выводим ответ.

for(i = 1; i <= n; i++)

printf("%d ",res[i]);

printf("\n");