2923. Tree

A rooted tree consisting of n vertices is given. Each vertex is painted in one of n colors. For each vertex v, determine the number of distinct colors that appear in the subtree rooted at v.

Input. The first line contains a single integer n (1 ≤ n ≤ 10⁶). The following n lines describe the vertices of the tree. The i-th line contains two integers p_i and c_i, where p_i is the parent of vertex i, and c_i is the color of vertex i (1 ≤ c_i ≤ n). For the root of the tree, p_i = 0.

Output. Print n integers – one for each vertex from 1 to n. For each vertex, print the number of distinct colors in the subtree rooted at that vertex.

Sample input	Sample output
5 2 1 3 2 0 3 3 3 2 1	1 2 3 1 1

SOLUTION

graphs, depth first search

Algorithm analysis

Perform a depth-first traversal of the tree starting from the root. For each vertex i, maintain a set s_i, which accumulates the colors of all vertices in the subtree rooted at i.

If j is a child of vertex i during the traversal, then the set s_j should be merged into s_i.

The number of distinct colors in the subtree rooted at vertex i is equal to the size (cardinality) of the set s_i.

Example

The color of each vertex is shown on the left. The set of colors in its subtree is shown on the right.

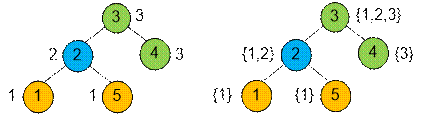
Algorithm implementation

The array color[i] stores the color of vertex i. The set s[i] will accumulate the colors that appear in the subtree rooted at vertex i.

The directed tree is represented as an adjacency list g. The array res[i] stores the number of distinct colors in the subtree rooted at vertex i.

#define MAX 1000010

int color[MAX], res[MAX];

set<int> s[MAX];

vector<vector<int> > g;

The function dfs performs a depth-first traversal of the tree starting from vertex v.

void dfs(int v)

{

First, the color of vertex v itself is added to the set s[v].

s[v].insert(color[v]);

Iterate over the tree edges (v, to).

for (int to : g[v])

{

dfs(to);

For each edge (v, to), merge the set s[to] into s[v]. If the size of s[v] is smaller than the size of s[to], swap them first. Then, the content of the smaller set s[to] is added to the larger set s[v].

if (s[v].size() < s[to].size()) s[v].swap(s[to]);

s[v].insert(s[to].begin(), s[to].end());

Clear the set s[to] – it is no longer needed.

s[to].clear();

}

After that, store the number of distinct colors in the subtree in res[v], which is the size of the set s[v].

res[v] = s[v].size();

}

The main part of the program. Read the input data.

scanf("%d",&n);

g.resize(n+1);

for(i = 1; i <= n; i++)

{

scanf("%d %d",&p,&c);

g[p].push_back(i);

color[i] = c;

}

Start the depth-first search from the root of the tree – the vertex with index 0.

dfs(0);

Print the answer.

for(i = 1; i <= n; i++)

printf("%d ",res[i]);

printf("\n");