2964. Магнитные подушки
Город будущего
застроен небоскрёбами, для передвижения между которыми и парковки транспорта
многие тройки небоскрёбов соединены треугольной подушкой из однополярных
магнитов. Каждая подушка соединяет ровно 3 небоскрёба и вид сверху на неё
представляет собой треугольник, с вершинами в небоскрёбах. Это позволяет
беспрепятственно передвигаться между соответствующими небоскрёбами. Подушки
можно делать на разных уровнях, поэтому один небоскрёб может быть соединён
различными подушками с парами других, причём два небоскрёба могут соединять
несколько подушек (как с разными третьими небоскрёбами, так и с одинаковыми).
Например, возможны две подушки на разных уровнях между небоскрёбами 1, 2 и 3,
и, кроме того, магнитная подушка между 1, 2, 5.
Система
магнитных подушек организована так, что с их помощью можно добираться от одного
небоскрёба, до любого другого в этом городе (с одной подушки на другую можно
перемещаться внутри небоскрёба), но поддержание каждой из них требует больших
затрат энергии.
Требуется
написать программу, которая определит, какие из магнитных подушек нельзя
удалять из подушечной системы города, так как удаление даже только такой
подушки может привести к тому, что найдутся небоскрёбы, из которых теперь
нельзя добраться до некоторых других небоскрёбов, и жителям станет очень
грустно.
Вход. В первой строке
находятся числа n и m (3 ≤ n ≤ 105, 1 ≤ m
≤ 105) –
количество небоскрёбов в городе и количество работающих магнитных подушек
соответственно. В каждой из последующих m
строк через пробел записаны три числа – номера небоскрёбов, соединённых
подушкой. Небоскрёбы пронумерованы числами от 1 до n. Гарантируется, что имеющиеся магнитные подушки позволяют
перемещаться от одного небоскрёба до любого другого.
Выход. Выведите
сначала количество тех магнитных подушек, отключение которых невозможно без
нарушения сообщения в городе. Если это число отлично от нуля, то в следующей
строке через пробел выведите их номера. Нумерация должна соответствовать тому
порядку, в котором подушки перечислены во входных данных. Нумерация начинается
с единицы.
|
Пример входа 1 |
Пример выхода 1 |
|
5 4 1 2 3 2 4 3 1 2 4 3 5 1 |
1 4 |
|
|
|
|
Пример входа 2 |
Пример выхода 2 |
|
3 2 1 2 3 3 2 1 |
0 |
|
|
|
|
Пример входа 3 |
Пример выхода 3 |
|
3 1 1 2 3 |
1 1 |
РЕШЕНИЕ
графы – точки сочленения
Анализ алгоритма
Для каждой
магнитной подушки введем дополнительную вершину, соединив ее с теми вершинами,
которые соединены этой самой подушкой. Пронумеруем новые вершины от n + 1 до n + m. Построенный граф
будет содержать m + n вершин. Далее найдем все точки
сочленения с номерами, большими n.
Если вершина i (i > n) – точка
сочленения, то это значит, что отключение магнитной подушки номер i – n
невозможно без нарушения сообщения в городе.
Пример
В первом примере
имеются 5 небоскрёбов и 4 магнитные подушки, расположенные как показано ниже.
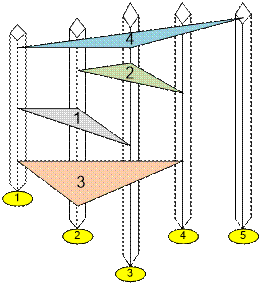
При отключении
подушки номер 4 небоскреб номер 5 будет отрезан от остальных домов.
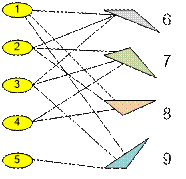
Построим граф из
5 + 4 = 9 вершин
как описано в анализе алгоритма. Полученный граф имеет одну точку
сочлененения 9, номер которой больше 5. Следовательно подушку номер 9 – 5 = 4 без
нарушения сообщения в городе удалять нельзя.
Реализация
алгоритма
Объявим
глобальные массивы. Граф храним в виде списка смежности в массиве graph.
vector<int> graph[MAX];
int used[MAX], d[MAX], up[MAX], ArtPoints[MAX];
Функция dfs совершает поиск в глубину, в котором строятся массивы d и up
и находятся точки сочленения. ArtPoints[v]
устанавливаем в 1, если вершина v –
точка сочленения. Иначе ArtPoints[v]
равно 0.
void dfs (int v, int p = -1)
{
used[v] = 1;
d[v] = up[v] = time++;
int children =
0;
for (int i = 0; i < graph[v].size(); i++)
{
int to =
graph[v][i];
if (to ==
p) continue;
if
(used[to])
up[v] = min (up[v], d[to]);
else
{
dfs (to, v);
up[v] = min (up[v], up[to]);
if
((up[to] >= d[v]) && (p != -1)) ArtPoints[v] = 1;
children++;
}
}
if ((p == -1)
&& (children > 1)) ArtPoints[v] = 1;
}
Основная часть
программы. Читаем входные данные. Строим граф.
scanf("%d %d",&n,&m);
Vertices = n + m;
memset(used,0,sizeof(used));
memset(d,0,sizeof(d));
memset(up,0,sizeof(up));
memset(ArtPoints,0,sizeof(ArtPoints));
for(i = 1; i <= m; i++)
{
scanf("%d %d
%d",&v1,&v2,&v3);
graph[n+i].push_back(v1);
graph[v1].push_back(n+i);
graph[n+i].push_back(v2);
graph[v2].push_back(n+i);
graph[n+i].push_back(v3);
graph[v3].push_back(n+i);
}
Запускаем поиск в глубину на графе, ищем все точки
сочленения.
time = 1;
for(i = 1; i <= Vertices; i++)
if (!used[i])
dfs(i);
Подсчитываем количество точек сочленения cntArtPoints.
int cntArtPoints = 0;
for(i = n + 1; i <= Vertices; i++)
if
(ArtPoints[i]) cntArtPoints++;
Выводим количество точек сочленения.
printf("%d\n",cntArtPoints);
Выводим номера магнитных подушек, удаление которых
невозможно без нарушения сообщения в городе.
if (cntArtPoints)
{
for (i = n + 1; i <= Vertices; i++)
if (ArtPoints[i]) printf("%d
", i - n);
printf("\n");
}
Java
реализация
import java.util.*;
public class Main
{
static ArrayList<Integer>[] g;
static int used[], up[], d[], ArtPoints[];
static int time;
static void dfs (int v, int p)
{
used[v] = 1;
d[v] = up[v] = time++;
int children = 0;
for (int i = 0; i < g[v].size(); i++)
{
int to = g[v].get(i);
if (to == p) continue;
if (used[to] == 1)
up[v] = Math.min(up[v], d[to]);
else
{
dfs (to, v);
up[v] = Math.min(up[v], up[to]);
if ((up[to] >= d[v]) && (p != -1)) ArtPoints[v] = 1;
children++;
}
}
if ((p == -1) && (children > 1)) ArtPoints[v] = 1;
}
@SuppressWarnings("unchecked")
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
g = new ArrayList[n+m+1]; // unchecked
used = new int[n+m+1];
up = new int[n+m+1];
d = new int[n+m+1];
ArtPoints = new int[n+m+1];
for (int i = 0; i <= n + m; i++)
g[i] = new ArrayList<Integer>();
for (int i = 1; i <= m; i++)
{
int v1 = con.nextInt();
int v2 = con.nextInt();
int v3 = con.nextInt();
g[n+i].add(v1); g[v1].add(n+i);
g[n+i].add(v2); g[v2].add(n+i);
g[n+i].add(v3); g[v3].add(n+i);
}
time = 1;
for(int i = 1; i <= n + m; i++)
if (used[i] == 0) dfs(i,-1);
int cntArtPoints = 0;
for(int i = n + 1; i <= n + m; i++)
if (ArtPoints[i] == 1) cntArtPoints++;
System.out.println(cntArtPoints);
if (cntArtPoints > 0)
{
for (int i = n + 1; i <= n + m; i++)
if (ArtPoints[i] == 1) System.out.print(i - n + "
");
System.out.println();
}
con.close();
}
}