2965. Расстояние между вершинами

Коль Дейкстру писать без кучи,

То тайм-лимит ты получишь...

А в совсем другой задаче

Юзай кучу Фибоначчи!

Задан неориентированный взвешенный граф. Найдите длину наименьшего пути между двумя заданными вершинами.

Вход. Первая строка содержит два натуральных числа n и m (1 ≤ n ≤ 10⁵, 1 ≤ m ≤ 2 * 10⁵) – количество вершин и рёбер в графе. Вторая строка содержит два натуральных числа s и t (1 ≤ s, t ≤ n, s ≠ t) – номера вершин, между которыми необходимо найти минимальный путь.

Следующие m строк содержат описание рёбер. Ребро номер i описывается тремя целыми числами b_i, e_i и w_i (1 ≤ b_i, e_i ≤ n, 0 ≤ w_i ≤ 100) – номера вершин, которые оно соединяет, и его вес.

Выход. Выведите вес минимального пути между вершинами s и t, или -1, если пути не существует.

Пример входа

Пример выхода

4 4

1 3

1 2 1

2 3 2

3 4 5

4 1 4

РЕШЕНИЕ

графы, алгоритм Дейкстры

Анализ алгоритма

Количество вершин в графе велико, поэтому для реализации алгоритма Дейкстры используем очередь с приоритетом.

Пример

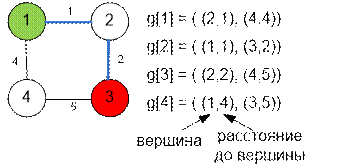
Граф, приведенный в примере, имеет вид:

Реализация алгоритма

Объявим константу бесконечность.

#define INF 0x3F3F3F3F

Объявим структуру g для хранения взвешенного графа. Каждый элемент g[i] является списком пар (вершина, расстояние).

vector<vector<pair<int, int> > > g;

Функция Dijkstra реализует алгоритм Дейкстры, начиная с вершины start.

void Dijkstra(vector<vector<pair<int, int>>>& g, vector<int>& d,

int start)

{

Объявим и инициализируем очередь с приоритетами pq. Элементами этой очереди будут пары (расстояние до вершины от истока, вершина). Таким образом, на вершине очереди всегда находится вершина графа с наименьшим расстоянием от истока.

priority_queue<pair<int, int>, vector<pair<int, int>>,

greater<pair<int, int>>> pq;

pq.push({0, start});

Инициализируем массив кратчайших расстояний d. Вершины графа нумеруются с 1 до n.

d = vector<int>(n + 1, INF);

d[start] = 0;

Продолжаем алгоритм Дейкстры, пока очередь не пустая.

while (!pq.empty())

{

Извлекаем пару e из вершины очереди с приоритетами.

pair<int, int> e = pq.top(); pq.pop();

int v = e.second; // node

Проверяем, является ли вершина v фиктивной. Если расстояние до v больше, чем уже вычисленное значение d[v], то игнорируем эту вершину.

if (e.first > d[v]) continue; // distance > d[v]

Перебираем все вершины to, смежные с v. Расстояние от v до to равно cost.

for (auto edge: g[v])

{

int to = edge.first;

int cost = edge.second;

Если ребро (v, to) релаксируется, то пересчитываем значение d[to] и заносим пару (d[to], to) в очередь.

if (d[v] + cost < d[to])

{

d[to] = d[v] + cost;

pq.push({d[to], to});

}

Основная часть программы. Читаем входные данные.

scanf("%d %d %d %d", &n, &m, &start, &fin);

g.resize(n + 1);

for (i = 0; i < m; i++)

{

Читаем неориентированное ребро (b, e) весом w и добавляем его в граф g.

scanf("%d %d %d", &b, &e, &w);

g[b].push_back({e, w});

g[e].push_back({b, w});

}

Запускаем алгоритм Дейкстры из стартовой вершины start.

Dijkstra(g, dist, start);

Выводим искомый кратчайший путь dist[fin]. Если dist[fin] равно бесконечности, то искомого пути не существует.

if (dist[fin] == INF)

printf("-1\n");

else

printf("%d\n", dist[fin]);

Реализация алгоритма – структура edge

Объявим константу бесконечность.

#define INF 0x3F3F3F3F

Объявим массив кратчайших расстояний dist.

vector<int> dist;

Структура edge хранит информацию о ребре: вершину node в которую оно идет и его вес dist.

struct edge

{

int node, dist;

edge(int node, int dist) : node(node), dist(dist) {}

};

Структура edge также будет использована в очереди с приоритетами. Очередь хранит вершины графа, где

· node – номер вершины;

· dist – текущее расстояние от начальной вершины до вершины node.

На вершине очереди будет находиться вершина графа с наименьшим значением dist.

bool operator< (edge a, edge b)

{

return a.dist > b.dist;

}

Объявим список смежности g графа.

vector<vector<edge> > g;

Функция Dijkstra реализует алгоритм Дейкстры, начиная с вершины start.

void Dijkstra(vector<vector<edge> > &g, vector<int> &d, int start)

{

priority_queue<edge> pq;

pq.push(edge(start, 0));

Инициализируем массив кратчайших расстояний d. Вершины графа нумеруются с 1 до n.

d = vector<int>(n + 1, INF);

d[start] = 0;

Продолжаем алгоритм Дейкстры, пока очередь не пустая.

while (!pq.empty())

{

Извлекаем пару e из вершины очереди с приоритетами.

edge e = pq.top(); pq.pop();

int v = e.node;

if (e.dist > d[v]) continue;

Перебираем все вершины to, смежные с v. Расстояние от v до to равно cost.

for (auto ed : g[v])

{

int to = ed.node;

int cost = ed.dist;

Если ребро (v, to) релаксируется, то пересчитываем значение d[to] и заносим пару (d[to], to) в очередь.

if (d[v] + cost < d[to])

{

d[to] = d[v] + cost;

pq.push(edge(to, d[to]));

}

Основная часть программы. Читаем входные данные.

scanf("%d %d %d %d", &n, &m, &start, &fin);

g.resize(n + 1);

for (i = 0; i < m; i++)

{

Читаем неориентированное ребро (b, e) весом w и добавляем его в граф g.

scanf("%d %d %d", &b, &e, &w);

g[b].push_back(edge(e, w));

g[e].push_back(edge(b, w));

}

Запускаем алгоритм Дейкстры из стартовой вершины start.

Dijkstra(g, dist, start);

Выводим искомый кратчайший путь dist[fin]. Если dist[fin] равно бесконечности, то искомого пути не существует.

if (dist[fin] == INF)

printf("-1\n");

else

printf("%d\n", dist[fin]);

Java реализация

import java.util.*;

class Node implements Comparator<Node>

{

public int node, dist;

Node() {}

Node(int node, int dist)

{

this.node = node;

this.dist = dist;

}

@Override

public int compare(Node a, Node b)

{

return a.dist - b.dist;

}

};

public class Main

{

// Adjacency list representation of the edges

static List<List<Node> > g;

static int dist[];

static int INF = Integer.MAX_VALUE;

static int n, m;

static void dijkstra(int start)

{

PriorityQueue<Node> pq = new PriorityQueue<Node>(n+1, new Node());

for (int i = 0; i <= n; i++)

dist[i] = Integer.MAX_VALUE;

// Add source node to the priority queue

pq.add(new Node(start, 0));

// Distance to the source is 0

dist[start] = 0;

while(!pq.isEmpty())

{

Node e = pq.poll();

int v = e.node;

if (e.dist > dist[v]) continue;

for(int j = 0; j < g.get(v).size(); j++)

{

int to = g.get(v).get(j).node;

int cost = g.get(v).get(j).dist;

if (dist[v] + cost < dist[to])

{

dist[to] = dist[v] + cost;

pq.add(new Node(to,dist[to]));

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

n = con.nextInt();

m = con.nextInt();

int start = con.nextInt();

int fin = con.nextInt();

g = new ArrayList<List<Node> >();

// Initialize list for every node

for (int i = 0; i <= n; i++)

{

List<Node> item = new ArrayList<Node>();

g.add(item);

}

for(int i = 0; i < m; i++)

{

int b = con.nextInt();

int e = con.nextInt();

int w = con.nextInt();

g.get(b).add(new Node(e,w));

g.get(e).add(new Node(b,w));

}

dist = new int[n+1];

dijkstra(start);

if (dist[fin] == INF)

System.out.println(-1);

else

System.out.println(dist[fin]);

con.close();

}

Python реализация

Импортируем очередь с приоритетом.

from queue import PriorityQueue

Объявим константу INF.

INF = 10**9

Функция Dijkstra реализует алгоритм Дейкстры, начиная с вершины start.

def dijkstra(graph, dist, start):

pq = PriorityQueue()

pq.put((0, start))

Инициализируем список кратчайших расстояний dist. Вершины графа нумеруются с 1 до n.

dist.extend([INF] * (n + 1))

dist[start] = 0

Продолжаем алгоритм Дейкстры, пока очередь не пустая.

while not pq.empty():

Извлекаем пару (cur_dist, v) из вершины очереди с приоритетами.

cur_dist, v = pq.get()

Проверяем, является ли вершина v фиктивной. Если расстояние до v больше, чем уже вычисленное значение dist[v], то игнорируем эту вершину.

if cur_dist > dist[v]: continue

Перебираем все вершины to, смежные с v. Расстояние от v до to равно cost.

for to, cost in graph[v]:

Если ребро (v, to) релаксируется, то пересчитываем значение d[to] и заносим пару (dist[to], to) в очередь.

if dist[v] + cost < dist[to]:

dist[to] = dist[v] + cost

pq.put((dist[to], to))

Основная часть программы. Читаем входные данные.

n, m = map(int, input().split())

start, fin = map(int, input().split())

g = [[] for _ in range(n + 1)]

for _ in range(m):

Читаем неориентированное ребро (b, e) весом w и добавляем его в граф g.

b, e, w = map(int, input().split())

g[b].append((e, w))

g[e].append((b, w))

Инициализируем список кратчайших расстояний dist.

dist = []

Запускаем алгоритм Дейкстры из стартовой вершины start.

dijkstra(g, dist, start)

Выводим искомый кратчайший путь dist[fin]. Если dist[fin] равно бесконечности, то искомого пути не существует.

if dist[fin] == INF:

print("-1")

else:

print(dist[fin])