2965. Distance between the vertices

An undirected weighted graph is given. Find the length of the shortest path between two specified vertices.

Input. The first line contains two positive integers n and m (1 ≤ n ≤ 10⁵, 1 ≤ m ≤ 2 * 10⁵) – the number of vertices and edges in the graph. The second line contains two positive integers s and t (1 ≤ s, t ≤ n, s ≠ t) – the numbers of the vertices between which you need to find the shortest path.

The following m lines contain the descriptions of the edges. Each edge i is described by three integers b_i, e_i, and w_i (1 ≤ b_i, e_i ≤ n, 0 ≤ w_i ≤ 100) – the numbers of the vertices it connects and its weight.

Output. Print the weight of the shortest path between vertices s and t, or −1 if no such path exists.

Sample input	Sample output
4 4 1 3 1 2 1 2 3 2 3 4 5 4 1 4	3

SOLUTION

graphs, Dijkstra algorithm

Algorithm analysis

The number of vertices in the graph is large, so we use a priority queue to implement Dijkstra’s algorithm.

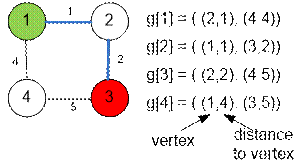
Example

The graph given in the example, has the following form:

Algorithm implementation

Declare a constant for infinity.

#define INF 0x3F3F3F3F

Declare a structure g for storing the weighted graph. Each element g[i] is a list of pairs (vertex, distance).

vector<vector<pair<int, int> > > g;

The function Dijkstra implements Dijkstra’s algorithm starting from the vertex start.

void Dijkstra(vector<vector<pair<int, int>>>& g, vector<int>& d,

int start)

{

Declare and initialize the priority queue pq. The elements of this queue will be pairs (distance from the source to the vertex, vertex). Thus, the vertex at the top of the queue will always be the one with the smallest distance from the source.

priority_queue<pair<int, int>, vector<pair<int, int>>,

greater<pair<int, int>>> pq;

pq.push({0, start});

Initialize the array of shortest distances d. The vertices of the graph are numbered from 1 to n.

d = vector<int>(n + 1, INF);

d[start] = 0;

Continue the Dijkstra’s algorithm until the queue is empty.

while (!pq.empty())

{

Extract the pair e from the top of the priority queue.

pair<int, int> e = pq.top(); pq.pop();

int v = e.second; // node

Check if the vertex v is a dummy vertex. If the distance to v is greater than the already computed value d[v], ignore this vertex.

if (e.first > d[v]) continue; // distance > d[v]

Iterate over all vertices to adjacent to v. The distance from v to to is cost.

for (auto edge: g[v])

{

int to = edge.first;

int cost = edge.second;

If the edge (v, to) relaxes, update the value of d[to] and insert the pair (d[to], to) into the queue.

if (d[v] + cost < d[to])

{

d[to] = d[v] + cost;

pq.push({d[to], to});

}

}

}

}

The main part of the program. Read the input data.

scanf("%d %d %d %d", &n, &m, &start, &fin);

g.resize(n + 1);

for (i = 0; i < m; i++)

{

Read the undirected edge (b, e) with weight w and add it to the graph g.

scanf("%d %d %d", &b, &e, &w);

g[b].push_back({e, w});

g[e].push_back({b, w});

}

Run Dijkstra’s algorithm from the starting vertex start.

Dijkstra(g, dist, start);

Print the shortest path distance dist[fin]. If dist[fin] is equal to infinity, then the path does not exist.

if (dist[fin] == INF)

printf("-1\n");

else

printf("%d\n", dist[fin]);

Algorithm implementation – edge structure

Declare a constant for infinity.

#define INF 0x3F3F3F3F

Declare an array of shortest distances dist.

vector<int> dist;

The edge structure stores information about an edge: the vertex node it leads to and its weight dist.

struct edge

{

int node, dist;

edge(int node, int dist) : node(node), dist(dist) {}

};

The edge structure will also be used in the priority queue. The queue stores the vertices of the graph, where:

· node is the vertex number;

· dist is the current distance from the start vertex to vertex node.

The vertex at the top of the queue will be the one with the smallest dist value.

bool operator< (edge a, edge b)

{

return a.dist > b.dist;

}

Declare the adjacency list g of the graph.

vector<vector<edge> > g;

The function Dijkstra implements Dijkstra’s algorithm starting from the vertex start.

void Dijkstra(vector<vector<edge> > &g, vector<int> &d, int start)

{

Declare and initialize the priority queue pq. The elements of this queue will be pairs (distance from the source to the vertex, vertex). Thus, the vertex at the top of the queue will always be the one with the smallest distance from the source.

priority_queue<edge> pq;

pq.push(edge(start, 0));

Initialize the array of shortest distances d. The vertices of the graph are numbered from 1 to n.

d = vector<int>(n + 1, INF);

d[start] = 0;

Continue the Dijkstra’s algorithm until the queue is empty.

while (!pq.empty())

{

Extract the pair e from the top of the priority queue.

edge e = pq.top(); pq.pop();

int v = e.node;

Check if the vertex v is a dummy vertex. If the distance to v is greater than the already computed value d[v], ignore this vertex.

if (e.dist > d[v]) continue;

Iterate over all vertices to adjacent to v. The distance from v to to is cost.

for (auto ed : g[v])

{

int to = ed.node;

int cost = ed.dist;

If the edge (v, to) relaxes, update the value of d[to] and insert the pair (d[to], to) into the queue.

if (d[v] + cost < d[to])

{

d[to] = d[v] + cost;

pq.push(edge(to, d[to]));

}

}

}

}

The main part of the program. Read the input data.

scanf("%d %d %d %d", &n, &m, &start, &fin);

g.resize(n + 1);

for (i = 0; i < m; i++)

{

Read the undirected edge (b, e) with weight w and add it to the graph g.

scanf("%d %d %d", &b, &e, &w);

g[b].push_back(edge(e, w));

g[e].push_back(edge(b, w));

}

Run Dijkstra’s algorithm from the starting vertex start.

Dijkstra(g, dist, start);

Print the shortest path distance dist[fin]. If dist[fin] is equal to infinity, then the path does not exist.

if (dist[fin] == INF)

printf("-1\n");

else

printf("%d\n", dist[fin]);

Java implementation

import java.util.*;

class Node implements Comparator<Node>

{

public int node, dist;

Node() {}

Node(int node, int dist)

{

this.node = node;

this.dist = dist;

}

@Override

public int compare(Node a, Node b)

{

return a.dist - b.dist;

}

};

public class Main

{

// Adjacency list representation of the edges

static List<List<Node> > g;

static int dist[];

static int INF = Integer.MAX_VALUE;

static int n, m;

static void dijkstra(int start)

{

PriorityQueue<Node> pq = new PriorityQueue<Node>(n+1, new Node());

for (int i = 0; i <= n; i++)

dist[i] = Integer.MAX_VALUE;

// Add source node to the priority queue

pq.add(new Node(start, 0));

// Distance to the source is 0

dist[start] = 0;

while(!pq.isEmpty())

{

Node e = pq.poll();

int v = e.node;

if (e.dist > dist[v]) continue;

for(int j = 0; j < g.get(v).size(); j++)

{

int to = g.get(v).get(j).node;

int cost = g.get(v).get(j).dist;

if (dist[v] + cost < dist[to])

{

dist[to] = dist[v] + cost;

pq.add(new Node(to,dist[to]));

}

}

}

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

n = con.nextInt();

m = con.nextInt();

int start = con.nextInt();

int fin = con.nextInt();

g = new ArrayList<List<Node> >();

// Initialize list for every node

for (int i = 0; i <= n; i++)

{

List<Node> item = new ArrayList<Node>();

g.add(item);

}

for(int i = 0; i < m; i++)

{

int b = con.nextInt();

int e = con.nextInt();

int w = con.nextInt();

g.get(b).add(new Node(e,w));

g.get(e).add(new Node(b,w));

}

dist = new int[n+1];

dijkstra(start);

if (dist[fin] == INF)

System.out.println(-1);

else

System.out.println(dist[fin]);

con.close();

}

}

Python implementation

Import the priority queue.

from queue import PriorityQueue

Declare a constant for infinity INF.

INF = 10**9

The function Dijkstra implements Dijkstra’s algorithm starting from the vertex start.

def dijkstra(graph, dist, start):

Declare and initialize the priority queue pq. The elements of this queue will be pairs (distance from the source to the vertex, vertex). Thus, the vertex at the top of the queue will always be the one with the smallest distance from the source.

pq = PriorityQueue()

pq.put((0, start))

Initialize the array of shortest distances dist. The vertices of the graph are numbered from 1 to n.

dist.extend([INF] * (n + 1))

dist[start] = 0

Continue the Dijkstra’s algorithm until the queue is empty.

while not pq.empty():

Extract the pair (cur_dist, v) from the top of the priority queue.

cur_dist, v = pq.get()

Check if the vertex v is a dummy vertex. If the distance to v is greater than the already computed value d[v], ignore this vertex.

if cur_dist > dist[v]: continue

Iterate over all vertices to adjacent to v. The distance from v to to is cost.

for to, cost in graph[v]:

If the edge (v, to) relaxes, update the value of d[to] and insert the pair (d[to], to) into the queue.

if dist[v] + cost < dist[to]:

dist[to] = dist[v] + cost

pq.put((dist[to], to))

The main part of the program. Read the input data.

n, m = map(int, input().split())

start, fin = map(int, input().split())

g = [[] for _ in range(n + 1)]

for _ in range(m):

Read the undirected edge (b, e) with weight w and add it to the graph g.

b, e, w = map(int, input().split())

g[b].append((e, w))

g[e].append((b, w))

Initialize the list of shortest distances dist.

dist = []

Run Dijkstra’s algorithm from the starting vertex start.

dijkstra(g, dist, start)

Print the shortest path distance dist[fin]. If dist[fin] is equal to infinity, then the path does not exist.

if dist[fin] == INF:

print("-1")

else:

print(dist[fin])