2967. День Объединения
В Байтландии
есть целых n городов, но нет ни одной
дороги. Король страны, Вольдемар де Беар, решил исправить эту ситуацию и
соединить некоторые города дорогами так, чтобы по этим дорогам можно было
добраться от любого города до любого другого. Когда строительство будет
завершено, король планирует отпраздновать День Объединения.
К сожалению,
казна Байтландии почти пуста, поэтому король требует сэкономить деньги,
минимизировав суммарную длину всех построенных дорог.
Вход. Первая строка
содержит количество n (1 ≤ n ≤ 5000) городов в Байтландии.
Каждая из следующих n строк содержит
по два целых числа xi, yi – координаты i-го города (-10000 ≤ xi, yi ≤ 10000). Никакие два города не расположены в
одной точке.
Выход. Вывести
минимальную суммарную длину дорог. Выведите ответ с точностью не менее 10-3.
|
Пример входа |
Пример выхода |
|
6 1 1 7 1 2 2 6 2 1 3 7 3 |
9.6568542495 |
РЕШЕНИЕ
графы – минимальное остовное дерево –
алгоритм Прима
Анализ алгоритма
Для решения
задачи следует найти минимальное остовное дерево. Реализуем алгоритм Прима.
Пример
Построим минимальное
остовное дерево для графа, приведенного в примере.
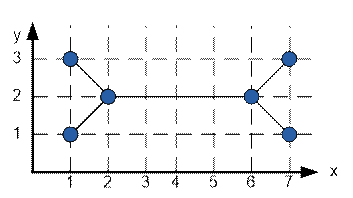
Величина
минимального остова равна 4 + 4![]() ≈ 9.65.
≈ 9.65.
Реализация
алгоритма
Объявим глобальные массивы. Координаты городов храним в (x[i], y[i]). Значение used[i]
= 1, если вершина i включена
в остов.
#define MAX 5001
#define INF 0x3F3F3F3F
int x[MAX], y[MAX];
int used[MAX], dist[MAX];
Функция dist2 вычисляет квадрат
расстояния между городами i и j.
int dist2(int i, int j)
{
return (x[j] - x[i])*(x[j] - x[i]) + (y[j] - y[i])*(y[j] - y[i]);
}
Функция Prim реализует алгоритм Прима и возвращает величину
минимального остова.
double Prim(void)
{
Инициализируем
массивы.
memset(dist, 0x3F,
sizeof(dist));
memset(used,
0, sizeof(used));
Начинаем строить минимальный остов с вершины 0. Инициализируем dist[0] = 0, used[0] = 1. В переменной
res вычисляем
величину минимального остова.
double res = 0;
int i, j, cur = 0;
dist[cur] = 0;
used[cur] =
1;
Совершаем n –
1 итерацию. На каждой итерации в остов добавляем одну вершину (так что в
остов еще следует добавить n – 1 вершин).
for (i = 1; i < n; i++)
{
Текущей вершиной является cur. Перебираем
ребра (cur, j) и
пересчитываем значение dist[j]. Таким
образом dist[j] хранит
текущее кратчайшее расстояние от вершины j до текущего минимального остова.
for (j = 0; j < n; j++)
if (!used[j] && (dist2(cur, j) < dist[j]))
dist[j] =
dist2(cur, j);
Ищем ребро наименьшей длины, которое будет включено в
остов. Для этого ищем такое наименьшее dist[j], что вершина j еще не
принадлежит остову (used[j]
= 0). Номер вершины с наименьшим dist[j] заносим в cur (она становится текущей).
int min = INF;
for (j = 0; j < n; j++)
if (!used[j] && (dist[j] < min))
{
min =
dist[j];
cur = j;
}
Вершина cur включается в
остов. Ребро длины sqrt(dist[cur]) добавляется
к остову.
used[cur] =
1;
res +=
sqrt(dist[cur]);
}
return res;
}
Основная
часть программы. Читаем входные данные.
scanf("%d", &n);
for (i = 0; i
< n; i++)
scanf("%d %d", &x[i], &y[i]);
Запускаем
алгоритм Прима и выводим
ответ.
res = Prim();
printf("%lf\n", res);
Реализация
алгоритма – min_e / end_e
Объявим глобальные
массивы. Координаты городов храним в (x[i],
y[i]).
#define MAX 5001
int x[MAX], y[MAX];
int used[MAX],
min_e[MAX], end_e[MAX];
Функция dist2 вычисляет
квадрат расстояния между городами i и
j.
int dist2(int i, int j)
{
return (x[j] - x[i])*(x[j] - x[i]) + (y[j] -
y[i])*(y[j] - y[i]);
}
Основная часть программы. Читаем координаты городов.
scanf("%d",&n);
for(i = 0; i <
n; i++)
scanf("%d %d",&x[i], &y[i]);
Инициализируем массивы.
memset(min_e,0x3F,sizeof(min_e));
memset(end_e,-1,sizeof(end_e));
memset(used,0,sizeof(used));
Величина минимального остова будет подсчитываться
в переменной dist.
dist = min_e[1] = 0;
for (i = 0; i <
n; i++)
{
Ищем вершину v с
минимальным значением min_e[v] среди еще не включенных в
минимальный остов вершин (для которых used[v]
= 0).
v = -1;
for (j = 0; j < n; j++)
if (!used[j] && (v == -1 || min_e[j] <
min_e[v])) v = j;
Включаем вершину v
в остов. Добавляем в остов ребро (v, end_e[v]).
used[v] = 1;
if (end_e[v] != -1) dist += sqrt((double)dist2(v,end_e[v]));
Пересчитываем метки для ребер, исходящих из v.
for (to = 0; to < n; to++)
{
int dV_TO = dist2(v,to);
if (!used[to] && (dV_TO < min_e[to]))
{
min_e[to] =
dV_TO;
end_e[to] = v;
}
}
}
Выводим величину минимального остова.
printf("%.6lf\n",dist);
Java
реализация
import java.util.*;
public class Main
{
static int x[], y[];
static int used[], min_e[], end_e[];
static int
dist2(int i, int j)
{
return (x[j] - x[i])*(x[j] - x[i]) + (y[j] - y[i])*(y[j] - y[i]);
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
x = new int[n];
y = new int[n];
for(int i = 0; i < n; i++)
{
x[i] = con.nextInt();
y[i] = con.nextInt();
}
min_e = new int[n];
Arrays.fill(min_e, Integer.MAX_VALUE);
end_e = new int[n];
Arrays.fill(end_e, -1);
used = new int[n];
double dist = min_e[1] = 0;
for (int i = 0; i < n; i++)
{
int v = -1;
for (int j = 0; j < n; j++)
if (used[j] == 0 && (v == -1 || min_e[j] < min_e[v])) v = j;
used[v] = 1;
if (end_e[v] != -1)
dist += Math.sqrt((double)dist2(v,end_e[v]));
for (int to = 0; to < n; to++)
{
int dV_TO = dist2(v,to);
if (used[to] == 0 && (dV_TO < min_e[to]))
{
min_e[to] = dV_TO;
end_e[to] = v;
}
}
}
System.out.println(dist);
con.close();
}
}