3004. Очередь

На железнодорожном вокзале работает k касс, однако очередь к ним всего одна. Обслуживание происходит следующим образом.

Сначала, когда все кассы свободны, первые k человек из очереди подходят к кассам. Остальные ожидают своей очереди. Как только одна из касс освобождается после обслуживания клиента, следующий по порядку человек из очереди занимает освободившееся место. Этот процесс продолжается, пока не будут обслужены все клиенты.

Определите время, за которое будут обслужены все клиенты.

Вход. Первая строка содержит два целых числа: размер очереди n и количество касс k (1 ≤ n ≤ 10⁵, 1 ≤ k ≤ 10⁴).

Вторая строка содержит n натуральных чисел t_i (1 ≤ t_i ≤ 10⁵) – время обслуживания i-го клиента.

Выход. Выведите одно число – минимальное время, необходимое для обслуживания всей очереди.

Пример входа	Пример выхода
7 3 1 2 3 4 5 3 1	7

РЕШЕНИЕ

структуры данных – set, куча

Анализ алгоритма

Будем моделировать процесс продажи билетов с помощью мультимножества s. Сначала подведём к свободным кассам первых k человек и занесём время их обслуживания в мультимножество.

В процессе работы мультимножество всегда будет содержать k элементов, каждый из которых обозначает момент времени, когда соответствующая касса освободится и сможет принять следующего клиента. Очевидно, что каждый новый человек должен подходить к той кассе, для которой этот момент минимален.

Время обслуживания последнего клиента будет являться искомым значением.

Пример

Рассмотрим приведенный пример. Сначала добавляем в кучу первые k = 3 элементов.

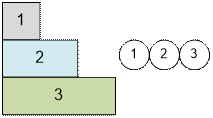
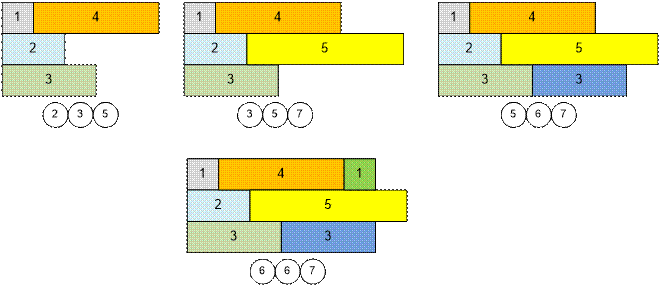
Далее на каждой итерации берем следующий элемент (следующего человека из очереди) и ставим его вместо наименьшего – в ту очередь, которая освободится раньше. В очередь добавляем время, когда этот новый человек завершит обслуживание на кассе.

Возле каждого рисунка указаны числа, находящиеся в куче.

Реализация алгоритма

Информацию о моментах времени, когда происходит продажа билетов в кассах, храним в мультимножестве s.

multiset<long long> s;

Читаем входные данные. Время обслуживания первых k человек заносим в s.

scanf("%d %d",&n,&k);

for(i = 0; i < n; i++)

{

scanf("%d",&ti);

if (s.size() != k) s.insert(ti);

else

{

Находим человека, который завершит обслуживание раньше всех, и ставим за ним следующего из очереди.

long long temp = *s.begin();

s.erase(s.begin());

s.insert(temp + ti);

}

}

Наибольшее число в мультимножестве s – это момент времени, когда будет обслужен последний клиент. Оно и является искомым значением.

while(s.size() > 1) s.erase(s.begin());

printf("%lld\n",*s.begin());

Реализация алгоритма – очередь с приоритетами

Создадим кучу, в вершине которой будет находиться наименьший элемент.

priority_queue<long long, vector<long long>, greater<long long> > pq;

Читаем входные данные. Время обслуживания первых k человек заносим в очередь pq.

scanf("%d %d",&n,&k);

for(i = 0; i < n; i++)

{

scanf("%d",&ti);

if (pq.size() != k) pq.push(ti);

else

{

Находим человека, который завершит обслуживание раньше всех, и ставим за ним следующего из очереди.

long long temp = pq.top(); pq.pop();

pq.push(temp + ti);

}

}

Наибольшее число в очереди pq – это момент времени, когда будет обслужен последний клиент. Оно и является искомым значением.

while(pq.size() > 1) pq.pop();

printf("%lld\n",pq.top());

Java реализация

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int k = con.nextInt();

PriorityQueue<Long> pq = new PriorityQueue<Long>();

for(int i = 0; i < n; i++)

{

long ti = con.nextLong();

if (pq.size() != k) pq.add(ti);

else pq.add(pq.poll() + ti);

}

while(pq.size() > 1) pq.poll();

System.out.println(pq.poll());

}

}