3058. Слоны

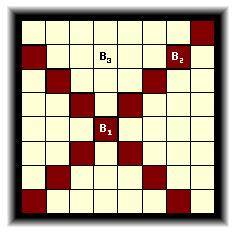
Слон – это шахматная фигура, которой играют на квадратной доске. Слон может передвигаться только по диагонали, а два слона могут атаковать друг друга, только если один из них находится на пути другого. На рисунке темными квадратами обозначены клетки, в которые может пойти слон B1 со своей текущей позиции. Слоны B1 и B2 атакуют друг друга, а B1 и B3 – нет. B2 и B3 не атакуют друг друга.

По заданным числам n и k определить количество способов, которыми можно расставить k слонов на шахматной доске размера n×n так, чтобы никакие два из них не били друг друга.

Вход. Каждая строка является отдельным тестом и содержит два целых числа n (1 ≤ n ≤ 30) и k (0 ≤ k ≤ n²). Последний тест содержит два нуля и не обрабатывается.

Выход. Для каждого теста в отдельной строке вывести количество способов, которыми можно расположить заданное число слонов на шахматной доске заданного размера так, чтобы никакие два слона не били друг друга. Известно, что ответ всегда будет меньше 10¹⁵.

Пример входа	Пример выхода
8 6 4 4 20 40 30 5 0 0	5599888 260 0 3127859642656

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Занумеруем диагонали шахматной доски следующим образом (рассмотрим доску 5×5):

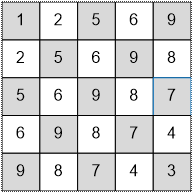
Черным диагоналям соответствуют нечетные номера, белым – четные. Диагонали пронумеруем в порядке увеличения количества клеток в них.

Обозначим через d[i][j] количество способов расставить j слонов на диагоналях от первой до i-ой включительно, причём только тех диагоналях, которые того же цвета, что и i-ая диагональ. Тогда 1 ≤ i ≤ 2n – 1 (доска размера n×n имеет 2n – 1 диагоналей), 0 ≤ j ≤ k.

Значение d[i][j] можно получить двумя способами:

· расставить j слонов на i – 2 предыдущих диагоналях (рассматриваем диагонали только того же цвета). Это можно совершить d[i – 2][j] способами.

· поставим одного слона на i-ую диагональ, а остальных j – 1 слонов разместим на i – 2 предыдущих диагоналях. Пусть на i-ой диагонали находится cells(i) клеток. Тогда ровно j – 1 из этих клеток будут под ударом j – 1 расставленного слона. То есть на i-ую диагональ можно поставить слона, который бы не находился под ударом остальных, в точности cells(i) – (j – 1) способами.

Таким образом

d[i][j] = d[i – 2][j] + d[i – 2][j – 1] * (cells(i) – j + 1)

Базу динамики определим следующим образом:

d[i][0] = 1, d[1][1] = 1

Чтобы расставить на шахматной доске k слонов можно, например, поставить i (0 ≤ i ≤ k) слонов на черных диагоналях и k – i слонов на белых. Тогда общее количество вариантов расстановки слонов равно

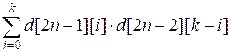
Отметим, что на шахматной доске размера n×n максимальный номер черной диагонали равен 2n – 1, а белой 2n – 2.

Реализация алгоритма

Объявим массив d для хранения вычислений.

long long d[60][3600];

Функция cells(i) возвращает количество клеток на i-ой диагонали.

int cells(int i)

{

if (i & 1) return i / 4 * 2 + 1;

else return (i - 1) / 4 * 2 + 2;

}

Основная часть программы. Если количество слонов k больше числа диагоналей 2n – 1, то решения не существует.

while(scanf("%d %d",&n,&k), n + k)

{

if (k > 2 * n - 1)

{

printf("0\n"); continue;

}

Инициализируем динамику.

for(i = 0; i <= 2 * n - 1; i++) d[i][0] = 1;

d[1][1] = 1;

Заполняем ячейки массива d согласно выше приведенной формуле.

for(i = 2; i <= 2 * n - 1; i++)

for(j = 1; j <= k; j++)

d[i][j] = d[i-2][j] + d[i-2][j-1] * (cells(i) - j + 1);

Можно поставить i слонов на черных диагоналях и k – i слонов на белых.. Количество слонов i перебираем от 0 до k.

res = 0;

for (i = 0; i <= k; i++)

res += d[n*2-1][i] * d[n*2-2][k-i];

Выводим ответ.

printf("%lld\n",res);

}