3061. Inner Vertices
There is an infinite square grid. Some
vertices of the grid are black and other vertices are white.
A vertex V is called inner if it is both
vertical-inner and horizontal-inner. A vertex V is called horizontal-inner if
there are two such black vertices in the same row that V is located between
them. A vertex V is called vertical-inner if there are two such black vertices
in the same column that V is located between them.
On each step all white inner vertices
became black while the other vertices preserve their colors. The process stops
when all the inner vertices are black.
Write a program that calculates a number of
black vertices after the process stops.
Input. The
first line of the input file contains one integer number n (0 ≤ n ≤
100000) – number of black vertices at the beginning.
The following n lines contain two integer numbers each – the coordinates of
different black vertices. The coordinates do not exceed 109 by their
absolute values.
Output. Print the number of black vertices when
the process stops. If the process does not stop, output -1.
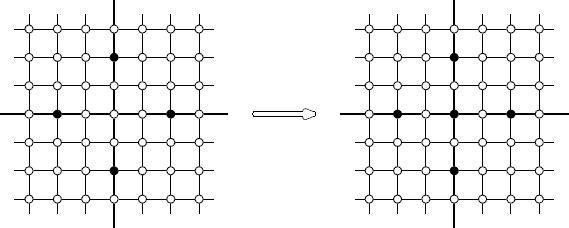
Sample
input
4
0 2
2 0
-2 0
0 -2
Sample
output
5
SOLUTION
data structures – дерево Фенвика
Анализ алгоритма
Поскольку количество входных черных вершин
не велико (порядка 105), а координаты вершин имеют порядок 109,
то изначально следует провести сжатие координат: например, перенумеровать
координаты таким образом, чтобы абсциссы и ординаты лежали в промежутке от 1 до
105.
Рассмотрим, например, следующий набор
входных данных:
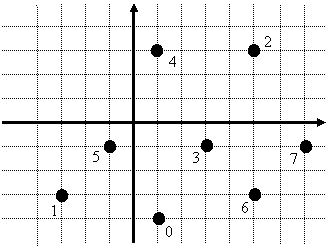
8
1
-4
-3
-3
5
3
3
-1
1
3
-1
-1
5
-3
7
-1
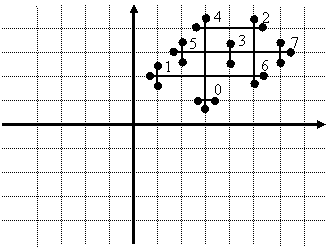
Возле каждой точки на рисунке указан ее
порядковый номер (начиная с нуля). Отсортируем абсциссы и ординаты точек по
возрастанию, после чего введем новую нумерацию абсцисс и ординат, начиная с
единицы.
|
новые абсциссы |
1 |
2 |
3 |
4 |
5 |
6 |
|
текущие абсциссы (x) |
–3 |
–1 |
1 |
3 |
5 |
7 |
|
текущие ординаты (y) |
–4 |
–3 |
–1 |
3 |
|
|
|
новые ординаты |
1 |
2 |
3 |
4 |
|
|
Таким образом, точка (–3, –3) будет
переименована в (1, 2), а точка (1, 3) в (3, 4). После описанного сжатия
координат исходные точки будут расположены на координатной плоскости следующим
образом:
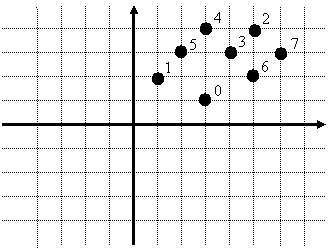
Пусть xmax
– максимальная абсцисса точек после преобразования координат, ymax – максимальная ордината точек.
Таким образом, координаты любой точки (xi,
yi) удовлетворяют
неравенствам: 1 ≤ xi
≤ xmax и 1 ≤ yi ≤ ymax.
Для каждой абсциссы xi соединим отрезком две крайние черные точки (с
минимальной и максимальной ординатой) с абсциссами xi. Такие же отрезки проведем и для каждой ординаты yi. Получим следующую
картинку:
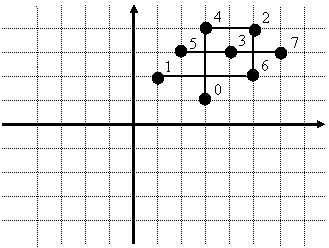
Например, с абсциссой x = 1 существует только одна черная точка с ординатой 2, поэтому
будем считать, что для абсциссы x = 1
построен вырожденный отрезок [2; 2]. То же самое касается и абсцисс x = 2, x = 4, x = 6. Для
абсциссы x = 3 получим отрезок [1; 4],
а для x = 5 отрезок [2; 4].
|
абсцисса |
1 |
2 |
3 |
4 |
5 |
6 |
|
отрезок |
[2; 2] |
[3; 3] |
[1; 4] |
[3; 3] |
[2; 4] |
[3; 3] |
Соответствующие отрезки для каждой из
ординат имеют вид:
|
ордината |
1 |
2 |
3 |
4 |
|
отрезок |
[3; 3] |
[1; 5] |
[2; 6] |
[3; 5] |
Если отобразить вырожденные отрезки, то
приведенная выше картинка будет иметь следующий вид:
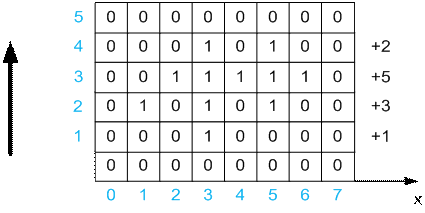
Из рисунка видно, что существует в точности
11 точек пересечения отрезков:
·
одна
точка по ординате y = 1 (абсцисса x = 3);
·
три
точки по ординате y = 2 (абсциссы x = 1, 3, 5);
·
пять
точек по ординате y = 3 (абсциссы x = 2, 3, 4, 5, 6);
·
две
точки по ординате y = 4 (абсциссы x = 3, 5);
Утверждение. Точка, лежащая на пересечении любых двух
отрезков, построенных описанным образом, на каком-то этапе преобразований
обязательно станет черной (если она таковой не была изначально).
Утверждение. Количество черных точек после окончания
процесса перекрашиваний равно количеству точек пересечений указанных отрезков.
Перекрашивания на каком-то этапе обязательно завершатся, так как ни одна точка
вне прямоугольника [1… xmax, 1… ymax] не может стать черной.
Утверждение. Количество точек пересечения вертикальных
и горизонтальных отрезков можно найти при помощи техники заметания прямой.
Будем, например, двигать прямую параллельно оси абсцисс, начиная с ординаты 1 и
заканчивая ординатой ymax.
Будем поддерживать массив b длины 105, характеризующий
состояние сканирующей прямой: b[i] =
1 если в абсциссе i уже начался
некоторый вертикальный отрезок, но еще не закончился. Рассмотрим, например,
вертикальный отрезок, нижняя точка которого имеет координаты (i, j1),
а верхняя (i, j2). Тогда при прохождении сканирующей прямой j1-ой горизонтали, мы
включаем в массив b этот отрезок,
устанавливая b[i] = 1. Когда
сканирующая прямая дойдет до (j2
+ 1)-ой горизонтали, исключаем отрезок из b,
устанавливая b[i] = 0.
Перед обработкой концов отрезков будем для
каждого состояния сканирующей прямой подсчитывать сумму чисел в массиве b – она равна количеству черных точек на
текущей горизонтали после окончания процесса перекрашивания. На рисунке справа
указана сумма единиц для каждой горизонтали. Итого в сумме имеем 11 черных
точек.
Реализация
алгоритма
Количество точек считываем в переменную n. Абсциссы точек сохраняем в массиве
xc, ординаты – в массиве yc. Зеленым цветом будем указывать состояния
переменных программы, запущенной на рассмотренном выше примере.
scanf("%d",&n);
for(i = 0; i < n; i++)
{
scanf("%d %d",&xx,&yy);
xc.push_back(xx); yc.push_back(yy);
}
// xc[8] = (1, -3,5,
3,1,-1, 5, 7)
// yc[8] =
(-4,-3,3,-1,3,-1,-3,-1)
Объявим множество set<int> temp, при помощи которого будем сортировать координаты и совершать сжатие
координат (сначала абсцисс, потом ординат). Занесем абсциссы точек во множество
temp, после чего поставим им во взаимно однозначное соответствие натуральные
числа, начиная с 1. Новые абсциссы сохраняем в отображении map<int,int> xn.
for(i = 0; i < xc.size(); i++) temp.insert(xc[i]);
for(Cnt = 1, iter = temp.begin(); iter != temp.end();
iter++)
xn[*iter] = Cnt++;
//xn[6] =
((-3,1),(-1,2),(1,3),(3,4),(5,5),(7,6))
Новые ординаты точек сохраняем в
отображении map<int,int> yn.
for(temp.clear(),i = 0; i < yc.size(); i++)
temp.insert(yc[i]);
for(Cnt = 1, iter = temp.begin(); iter != temp.end();
iter++)
yn[*iter] = Cnt++;
// yn[4] =
((-4,1),(-3,2),(-1,3),(3,4))
Занесем новые координаты точек в массив vector<pair<int,int> > p:
for(i = 0; i < n; i++)
p.push_back(make_pair(xn[xc[i]],yn[yc[i]]));
// p[8] =
((3,1),(1,2),(5,4),(4,3),(3,4),(2,3),(5,2),(6,3))
Количество входных черных вершин не более
105, следовательно, длины отображений xn и yn будут не более 100000.
Максимальные и минимальные значения ординат для каждой абсциссы храним в
массивах vector<int>
MinY(MAX,INF), MaxY(MAX,-1),
где значение INF установим равным 106, а MAX равным 105 +
1. Соответственно максимальные и минимальные значения абсцисс для каждой
ординаты храним в массивах vector<int>
MinX(MAX,INF), MaxX(MAX,-1).
for(i = 0; i < n; i++)
{
if (p[i].second < MinY[p[i].first]) MinY[p[i].first] = p[i].second;
if (p[i].second > MaxY[p[i].first]) MaxY[p[i].first] = p[i].second;
if (p[i].first <
MinX[p[i].second]) MinX[p[i].second] = p[i].first;
if (p[i].first >
MaxX[p[i].second]) MaxX[p[i].second] = p[i].first;
}
// MinY[100001] = (1000000,2,3,1,3,2,3,1000000,...)
// MaxY[100001] = (-1,
2,3,4,3,4,3,-1,...)
// MinX[100001] = (1000000,3,1,2,3,1000000,...)
// MaxX[100001] = (-1,
3,5,6,5,-1,...)
Занесем в отображение map<int,vector<int>
> m следующую информацию: с каждой ординатой yi (для нашего теста таких
ординат четыре: 1, 2, 3, 4) свяжем массив, содержащий абсциссы точек с
ординатой yi. При этом
абсциссы будем записывать со знаком плюс, если они соответствуют нижней точке
вертикального отрезка и минус, если верхней.
Например, рассмотрим горизонталь y = 2. На ней начинаются отрезки с
абсциссами x = 1 и x = 5. В то же время на горизонтали y = 2 заканчивается отрезок с абсциссой x = 1. Таким образом, ординате 2
необходимо поставить в соответствие массив {1, 5, –1}.
for(i = 1; MinY[i] != INF; i++)
m[MinY[i]].push_back(i);
for(i = 1; MaxY[i] != -1; i++)
m[MaxY[i]].push_back(-i);
// m[4] =
((1,[1](3)),(2,[3](1,5,-1)),(3,[6](2,4,6,-2,-4,-6)),
(4,[2](-3,-5)))
Остается найти количество точек пересечения
отрезков, используя метод заметания прямой. Для хранения информации о состоянии
прямой будем использовать дерево Фенвика. Реализуем следующие функции обработки
массива а:
·
функция
void inc(int
i, int delta) увеличивает элемент a[i] на delta;
·
функция
int sum(int
l, int r) возвращает сумму a[l] + a[l + 1] + … + a[r];
Будем двигать прямую параллельно оси
абсцисс вверх, начиная с ординаты i =
1. То есть последовательно просматривать вектора m[1], m[2], m[3], … . В
переменной res накапливаем количество
точек пересечения отрезков.
Значения m[i] присваиваются вектору temp и просматриваются слева направо. Если
значение temp[j] > 0, то в точке
(temp[j], i) начинается вертикальный отрезок. Увеличиваем на единицу temp[j] - ую ячейку массива a.
res = 0;
for(i = 1; MinX[i] != INF; i++)
{
vector<int> temp = m[i];
for(j = 0; j < temp.size(); j++)
if (temp[j] > 0) inc(temp[j],1);
Находим количество точек пересечения,
имеющих ординату i, выполняя запрос sum(MinX[i],MaxX[i]) и добавляем возвращаемое значение к res.
res +=
sum(MinX[i],MaxX[i]);
Снова просматриваем массив temp слева
направо. Если temp[j] < 0, то в
точке (temp[j], i) заканчивается вертикальный отрезок. Уменьшаем на единицу –temp[j] - ый элемент массива a.
for(j = 0; j < temp.size(); j++)
if (temp[j] < 0) inc(-temp[j],-1);
}
Выводим результат на печать.
printf("%d\n",res);