3165. Двухцветность

В 1976 году “Теорема четырёх красок” была доказана с помощью компьютера. Эта теорема утверждает, что каждая карта может быть окрашена с использованием только четырех цветов таким образом, что ни одна область не будет окрашена тем же цветом, что и ее соседние.

Вам предлагается решить подобную задачу, но попроще. Необходимо выяснить, является ли заданный связный граф двухцветным. То есть можно ли его вершинам назначить цвета (имеется всего два цвета) таким образом, чтобы никакие две смежные вершины не имели одинаковый цвет. Для упрощения задачи можно предположить, что:

· граф не имеет петель.

· граф неориентированный. То есть если вершина a связана с вершиной b, то и b связана с a.

· граф сильно связный. То есть всегда существует как минимум один путь из любой вершины в любою другую.

Вход. Состоит из нескольких тестов. Каждый тест начинается со строки, содержащей количество вершин n (0 ≤ n ≤ 1000). Вторая строка содержит количество рёбер l (1 ≤ l ≤ 250000). После этого идёт l строк, каждая из которых содержит два числа, указывающие на ребро между двумя вершинами, которые оно соединяет. Вершины в графе будут помечены числом a (1 ≤ a ≤ n). Последний тест содержит n = 0 и не обрабатывается.

Выход. Выяснить, можно ли сделать входной граф двухцветным и вывести соответствующее сообщение, как показано в примере.

Пример входа	Пример выхода
3 3 1 2 2 3 3 1 8 12 1 2 2 4 3 4 3 1 3 7 7 6 4 6 1 6 2 5 5 6 4 8 5 8 0	NOT BICOLOURABLE. BICOLOURABLE.

РЕШЕНИЕ

поиск в глубину

Анализ алгоритма

Для решения задачи воспользуемся поиском в глубину. Изначально вершины не просмотрены, пометим их все цветом 0. По мере прохождения по вершинам будем красить их в два цвета: 1 и 2. Если текущая вершина имеет цвет i (i = 1, 2), то следующую вершину, в которую мы попадаем при поиске в глубину, красим в цвет 3 – i. При этом проверяем, чтобы две соседние вершины не были покрашены в одинаковый цвет.

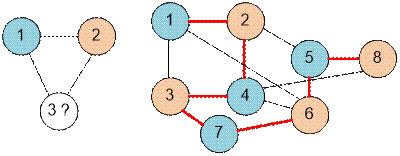
Пример

Приведенные в примере графы имеют вид:

Реализация алгоритма

Матрицу смежности графа храним в массиве g размера MAX = 1001 (нумерация вершин идет от 1 до n ≤ 1000). Массив used содержит информацию о цвете вершины. Глобальная переменная Error отвечает за правильность раскраски: как только найдутся две соседние вершины, покрашенные одинаково, переменная примет значение 1.

#define MAX 1000

int g[MAX][MAX], used[MAX], Error;

Функция dfs выполняет поиск в глубину. Ей передаются два параметра: текущая вершина v и ее цвет color. Если уже встретился случай невозможности требуемой раскраски (Error = 1), то следует выйти из функции.

void dfs(int v,int color)

{

Если уже встретился случай невозможности требуемой раскраски (Error = 1), то следует выйти из функции.

if (Error) return;

Помечаем вершину v цветом color.

used[v] = color;

Ищем непросмотренную вершину i, в которую можно пойти, продолжив поиск в глубину. При этом если соседняя вершина i уже была просмотрена, проверяем условие окрашенности вершин v и i в разные цвета. Если указанные вершины покрашены в одинаковый цвет, устанавливаем Error = 1.

for(int i = 1; i <= n; i++)

if (g[v][i] == 1)

if (used[i] == 0) dfs(i,3-color); else

if (used[v] == used[i]) Error = 1;

}

Основной цикл программы. Читаем число вершин n и количество ребер l графа. Обнуляем матрицу смежности и массив used.

while(scanf("%d %d",&n,&l), n)

{

memset(g,0,sizeof(g));

memset(used,0,sizeof(used));

Читаем данные графа.

for(i = 0; i < l; i++)

{

scanf("%d %d",&a,&b);

g[a][b] = g[b][a] = 1;

}

Обнуляем значение переменной Error, запускаем поиск в глубину с первой вершины, покрасив ее изначально в цвет 1.

Error = 0; dfs(1,1);

В зависимости от значения переменной Error выводим результат.

if (Error) printf("NOT BICOLOURABLE.\n");

else printf("BICOLOURABLE.\n");

}

Java реализация

import java.util.*;

public class Main

{

static int g[][], used[];

static int n, l, Error;

static void dfs(int v,int color)

{

if (Error == 1) return;

used[v] = color;

for(int i = 1; i <= n; i++)

if (g[v][i] == 1)

{

if (used[i] == 0) dfs(i,3-color);else

if (used[v] == used[i]) Error = 1;

}

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

while(true)

{

n = con.nextInt();

if (n == 0) break;

l = con.nextInt();

g = new int[n+1][n+1];

used = new int[n+1];

for(int i = 0; i < l; i++)

{

int a = con.nextInt();

int b = con.nextInt();

g[a][b] = g[b][a] = 1;

}

Error = 0;

dfs(1,1);

if (Error == 1) System.out.println("NOT BICOLOURABLE.");

else System.out.println("BICOLOURABLE.");

}

con.close();

}

}