3174. North East King
There is a king
in the lower left corner of the n ×
n checkmate board. The king can
move one step right, one step up or diagonally one step up-right. How many ways
are there for him to reach the upper right corner of the board?
Input. The first line contains the number of test
cases t (1 ≤ t ≤ 1000). The next t lines consist of single integer n (1 ≤ n ≤ 1000) Ц the size of the board.
Output. For each test case output in a separate line
the number of ways to reach upper right corner of n × n board
modulo 1000003.
|
Sample
input |
Sample
output |
|
2 2 3 |
3 13 |
SOLUTION
dynamic programming
Algorithm analysis
From any square,
the king can move one square to the right, up, or diagonally up to the right.
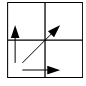
Let dp be a two dimensional array where dp[i][j] is equal to the number of ways the king
can get from (1, 1) to (i, j). Set dp[1][1] = 1.
The king can
enter the cell (i, j)
either from (i Ц 1, j) or from (i, j Ц 1) or from (i Ц 1, j Ц 1). Therefore
dp[i][j]
= dp[i Ц 1][j] + dp[i][j Ц 1] + dp[i Ц 1][j Ц 1]
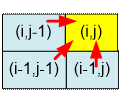
Initially, set the dp array to zero. For us, zeroing the zero
row and zero column of the dp array
will be essential. If, for example, i
= 1, then dp[i Ц 1][j] = dp[0][j] = 0 and the
equation of dynamics turns into dp[i][j] = dp[i][j Ц 1] (this is how the first line is
recomputed). If j = 1, then the
equation of dynamics will take the form dp[i][j] = dp[i Ц 1][j] (this is how
the first column is recomputed). Considering that dp[1][1] = 1, we can conclude that the
first column and the first row in all cells will contain 1.
Example
Fill the dp array for a field of size 4 * 4:

Algorithm realization
Declare the array dp.
#define MAX 1001
#define MOD 1000003
int dp[MAX][MAX];
Fill the cellls of array dp.
memset(dp, 0, sizeof(dp));
dp[0][0] = 1;
for (i = 1; i < MAX; i++)
for (j = 1; j < MAX; j++)
† dp[i][j]
= (dp[i - 1][j] + dp[i][j - 1] + dp[i - 1][j - 1]) % MOD;
Read the input data. For each input value of n print dp[n][n].
scanf("%d", &tests);
while (tests--)
{
† scanf("%d", &n);
† printf("%d\n", dp[n][n]);
}