3239. Функция Мертенса

Функция Мёбиуса μ(n) – мультипликативная функция, названная так в честь известного математика девятнадцатого столетия Августа Мёбиуса, знаменитого также своей лентой. Определяется функция следующим рекуррентным соотношением:

μ(1) = 1,

Функция Мёбиуса связана с функцией Мертенса соотношением:

M(n) =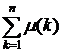

Требуется найти значение функции Мертенса по заданному числу n.

Вход. В первой строке задано количество тестов t (1 ≤ t ≤ 100000). Каждый тест состоит из единственного числа n (1 ≤ n ≤ 10⁷).

Выход. Для каждого теста в отдельной строке выведите единственное число, являющееся ответом к задаче.

Пример входа	Пример выхода
4 2 1 4 7	0 1 -1 -2

РЕШЕНИЕ

функция Мебиуса

Анализ алгоритма

Реализуем решето Мебиуса за линейное время. Вычислим значение функции Мертенса для всех значений от 1 до 10⁷.

Реализация алгоритма

Объявим константы и глобальные массивы.

#define MAX 10000010

#define LMAX 700000

int lp[MAX+1] = {0}, primes[LMAX];

char mu[MAX] = {0};

Линейный Эратосфен. lp[i] содержит наименьший простой делитель числа i.

void LinearEratosfen(void)

{

int i, j;

for (i = 2; i <= MAX; ++i)

{

if (lp[i] == 0)

{

lp[i] = i;

primes[cnt++] = i;

}

for (j = 0; j < cnt && primes[j] <= lp[i] &&

i * primes[j] <= MAX; j++)

lp[i * primes[j]] = primes[j];

}

}

Вычисление функции Мебиуса используя массив lp.

void calc_Mobius(void)

{

int i, q;

mu[1] = 1;

for(i = 2; i < MAX; i++)

{

q = i / lp[i];

if (q % lp[i] != 0) mu[i] = -mu[q];

}

В массиве lp вычисляем значение функции Мертенса (чтобы не вводить новый линейный массив, таким образом сэкономив память).

lp[1] = mu[1];

for(i = 2; i < MAX; i++) lp[i] = lp[i-1] + mu[i];

}

Основная часть программы. Вычисляем функцию Мертенса для всех значений от 1 до 10⁷.

LinearEratosfen();

calc_Mobius();

Читаем входные данные. Для каждого значения n выводим lp[n].

scanf("%d",&tests);

while(tests--)

{

scanf("%d",&n);

printf("%d\n",lp[n]);

}