3298. Общий предок

Дан ориентированный граф. Подсчитайте, сколько пар вершин (i, j) имеют общего предка. Общим предком вершин i и j называется такая вершина k, что и i и j достижимы из k.

Вход. В первой строке содержатся целые числа n и m (1 ≤ n ≤ 10⁴, 0 ≤ m ≤ 10⁴) – количество вершин и рёбер в графе. Далее следуют m строк по два числа от 1 до n в каждой. Пара чисел (a, b) означает, что из вершины a есть ребро в вершину b.

Выход. Выведите одно число – количество пар.

Пример входа	Пример выхода
3 2 2 1 3 1	7

РЕШЕНИЕ

LCA – поиск в ширину

Анализ алгоритма

Для каждого значения i (1 ≤ i ≤ n) подсчитаем, сколько пар вершин (i, j) имеют общего предка. Если вершина j достижима из i, то общим предком (i, j) будет i. Если общим предком (i, j) является вершина k, то из i в k существует путь по ребрам транспонированного графа, а из k в j по ребрам имеющегося графа.

Запустим из вершины i поиск в ширину по ребрам транспонированного графа. Таким образом мы попадем во все возможные вершины k. При этом пройденные вершины не удаляем из очереди, а сохраняем в ней. По окончанию поиска в ширину очередь содержит вершины, которые являются общим предком (i, j).

Теперь запустим из вершин, находящихся в очереди, поиск в ширину по ребрам исходного графа. Выполняя этот поиск, мы попадем во все такие j, что общим предком (i, j) является вершина k, достижимая из i по ребрам транспонированного графа.

Осталось подсчитать количество вершин, достижимых из i в результате выполнения двух описанных поисков в ширину. Оно равно количеству пар (i, j), которые имеют общего предка.

Пример

Входной граф имеет вид:

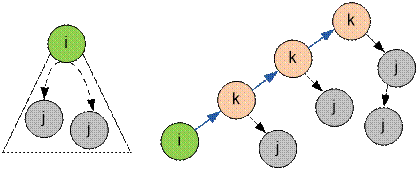
Оранжевым цветом обозначены вершины, достижимые из v (при вызове bfs(v)) по ребрам транспонированного графа. Желтым обозначены вершины, достижимые из оранжевых по ребрам исходного графа. Справа указаны пары вершин (одна из которых равна v), имеющие общего предка.

Итого имеется 7 пар (i, j), которые имеют общего предка.

Реализация алгоритма

Граф храним в массиве g, транспонированный – в массиве gr. Для ускорения работы программы количество ребер, исходящих из вершины i графа (фактически значение g[i].size()), сохраним в gSize[i]. Аналогично значения gr[i].size() сохраним в grSize[i]. Массив used используется при поиске в ширину.

#define MAX 10001

vector<int> g[MAX], gr[MAX];

int used[MAX], gSize[MAX], grSize[MAX];

Запускаем сначала поиск в ширину из вершины v по ребрам транспонированного графа. Все пройденные вершины сохраняются в массиве (очереди) Q.

void bfs(int v)

{

int Q[MAX], qh = 0, qt = 1;

Q[0] = v; used[v] = 1;

while(qh < qt)

{

int u = Q[qh++];

for(int i = 0; i < grSize[u]; i++)

{

int to = gr[u][i];

if(!used[to])

{

used[to] = 1; Q[qt++] = to;

}

}

}

Запускаем поиск в ширину из вершин, хранящихся в очереди Q, по ребрам исходного графа.

qh = 0;

while(qh < qt)

{

int u = Q[qh++];

for(int i = 0; i < gSize[u]; i++)

{

int to = g[u][i];

if(!used[to])

{

used[to] = 1; Q[qt++] = to;

}

}

}

}

Основная часть программы. Читаем входные данные.

scanf("%d %d",&n,&m);

memset(gSize,0,sizeof(gSize));

memset(grSize,0,sizeof(grSize));

for(i = 0; i < m; i++)

{

scanf("%d %d",&u,&v);

g[u].push_back(v); gr[v].push_back(u);

gSize[u]++; grSize[v]++;

}

Последовательно запускаем поиск в ширину из вершин 1, 2, …, n. Для каждой вершины i после вызова bfs(i) подсчитываем при помощи массива used количество вершин j таких, что для (i, j) имеется общий предок (оно равно числу таких j, для которых used[j] = 1).

for(i = 1; i <= n; i++)

{

memset(used,0,sizeof(used));

bfs(i);

for(j = 1; j <= n; j++)

if (used[j]) res++;

}

Выводим результат.

printf("%d\n",res);