3326. Создание
Бинарного Дерева Поиска
Бинарным деревом
поиска (БДП) является дерево с корнем, обладающее следующими свойствами:
·
Левое поддерево содержит только вершины, значения которых
строго меньшие корня.
·
Правое поддерево содержит только вершины, значения которых
строго больше корня.
·
Все значения вершин разные.
·
Левое и правое поддерево рекурсивно является бинарным
деревом поиска.
При вставке
новой вершины запускается следующий алгоритм:
1. Если дерево
пустое, то новая вершина становится корнем и процесс вставки заканчивается.
Иначе перейти на шаг 2.
2. Объявим
текущей вершиной корень дерева.
3. Если значение
новой вершины меньше корня, то:
·
Если левое поддерево корня пусто, то установим новую
вершину левым сыном корня и останавливаемся.
·
Иначе установим текущей вершиной корень левого поддерева и
повторим шаг 3.
4. Если значение
новой вершины больше корня, то:
·
Если правое поддерево корня пусто, то установим новую
вершину правым сыном корня и останавливаемся.
·
Иначе установим текущей вершиной корень правого поддерева
и повторим шаг 3.
Структура БДП
зависит от входной последовательности. Разные последовательности могут
порождать разные структуры, несмотря на то что числа в них одинаковые.
Рассмотрим
последовательность 1 2 3. Получим следующее БДП:
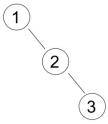
Если входная
последовательность имеет вид 2 1 3, то получим дерево
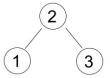
С другой
стороны, разные входные данные могут порождать одинаковые БДП структуры. Например,
входная последовательность 2 1 3 породит ту же структуру БДП, что и
последовательность 4 6 2. Дерево будет иметь вид:
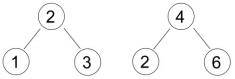
По заданным n вершинам БДП определить, сколько
различных входных последовательностей образуют ту же самую БДП структуру, что и
заданная. Вершины дерева принимают значения из диапазона 1..m.
Вход. Первая строка содержит количество тестов t (t
≤ 100). Каждый тест начинается с двух целых чисел n и m (1 ≤ n ≤ m ≤ 1000) – количество вершин в БДП и максимальное значение
диапазона соответственно. Следующая строка содержит n целых чисел ai
(1 ≤ ai ≤
1000) – последовательность, из которой строится БДП.
Выход. Для каждого теста вывести количество разных
последовательностей, образующих ту же самую БДП структуру, что и входная
последовательность. Вершины дерева принимают значения из диапазона 1..m. Результат следует выводить по модулю
1,000,003.
|
Пример
входа |
Пример
выхода |
|
3 3 4 1 2 3 3 4 3 1 4 5 6 3 1 5 4 6 |
4 8 48 |
РЕШЕНИЕ
рекурсия
Анализ алгоритма
Имеется бинарное
дерево поиска с n вершинами.
Необходимо найти количество последовательностей (порядков вставки вершин),
которые образуют такую же структуру. Поскольку вершины дерева могут принимать m значений, а само дерево содержит
только n вершин (n ≤ m), то имеется 
вариантов выборки этих
n значений.
Рассмотрим
некоторую последовательность вставок, которая генерирует дерево с корнем v. Пусть левое поддерево корня имеет nLeft вершин, а правое nRight вершин. Естественно, что корень v дерева всегда находится в начале
последовательности. Метки вершин, попадающие в левое поддерево, объединим в
список А. Метки вершин правого поддерева
объединим в список B. Рассмотрим nLeft
+ nRight чисел последовательности без
корня v. Между собой числа из разных
списков можно переставлять как угодно (нельзя менять относительный порядок чисел
одного списка), при этом структура дерева будет получаться одна и та же. То
есть 
различных
последовательностей образуют одну и ту же структуру.
Остается для
каждой вершины дерева посчитать количество вершин в ее левом и правом
поддереве. После чего перемножить значения для всех вершин
построенного дерева. Для получения окончательного ответа следует умножить
полученное произведение на . Все вычисления проводятся по модулю 1.000.003.
Пример
Рассмотрим
третий тест. После вставки всех вершин получим следующее дерево:
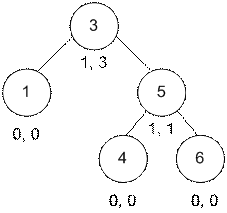
Под каждой
вершиной записано два числа: количество вершин в ее левом nLeft и правом nRight поддереве.
Остается перемножить значения всех вершин, а
полученное произведение еще умножить на . Ответом задачи будет число
(
*
*
**) * 
= (4 * 2 * 1 * 1 * 1)
* 6 = 48
Рассмотрим
корень v = 3, список А = {1} и список
B = {5, 4, 6}. Построим последовательность, первым числом которого будет 3, а
далее идут числа из списков А и В. При этом будем сохранять относительный
порядок чисел каждого списка. Такой последовательностью может быть одна из
следующих:
|
3, 1, 5, 4, 6 |
3, 5, 1, 4, 6 |
3, 5, 4, 1, 6 |
3, 5, 4, 6, 1 |
Для поддерева с
корнем v = 5 получим два списка А =
{4} и B = {6}. Это значит, что в любой из построенных последовательностей,
генерирующей требуемую структуру, можно переставлять между собой числа 4 и 6.
Таким образом получим следующие последовательности:
|
3, 1, 5, 4, 6 |
3, 5, 1, 4, 6 |
3, 5, 4, 1, 6 |
3, 5, 4, 6, 1 |
|
3, 1, 5, 6, 4 |
3, 5, 1, 6, 4 |
3, 5, 6, 1, 4 |
3, 5, 6, 4, 1 |
Реализация
алгоритма
Объявим
вспомогательные константы.
#define MOD 1000003
#define MAX 1001
Вершина дерева описывается структурой tree. В переменных nLeft
и nRight содержится соответственно
количество вершин в левом и правом поддереве.
struct tree
{
int data, nLeft, nRight;
struct tree *left, *right;
} *t;
В массив cnk заносятся значения биномиальных коэффициентов: 
= cnk[n][k].
long long cnk[MAX][MAX];
long long c(int n, int k)
{
if (cnk[n][k] > 0) return
cnk[n][k];
if (n - k < k) return
c(n,n-k);
if (!k) return
cnk[n][k] = 1;
return cnk[n][k] = (c(n-1,k) + c(n-1,k-1)) % MOD;
}
Вставка новой вершины со значением data в дерево T. При вставке нового элемента в левое или правое
поддерево увеличиваем в корне на единицу соответственно значение nLeft или nRight.
void insert(struct tree *&T,int data)
{
if (!T)
{
T = new tree;
T->data = data; T->left = T->right = NULL;
T->nLeft = T->nRight = 0;
return;
}
if (data < T->data)
{
(T->nLeft)++;
insert(T->left,data);
}
else
{
(T->nRight)++;
insert(T->right,data);
}
}
Обход дерева слева направо.
void InOrder(struct tree *t)
{
if (!t) return;
InOrder(t->left);
res = (res * c(t->nLeft + t->nRight, t->nLeft)) % MOD;
InOrder(t->right);
}
Удаление дерева, освобождение памяти.
void Delete(struct tree *t)
{
if (t->left != NULL) Delete(t->left);
if (t->right != NULL) Delete(t->right);
delete t;
}
Основная часть программы. Читаем входные
данные. Из входной последовательности строим двоичное дерево поиска.
Одновременно для каждого узла подсчитываем количество вершин в левом и правом
поддереве.
scanf("%d",&tests);
while(tests--)
{
scanf("%d %d",&n,&m);
for(i = 0; i < n; i++)
scanf("%d",&value),
insert(t,value);
Вычисляем и выводим результат.
res = c(m,n); InOrder(t);
printf("%lld\n",res);
Чистим память, отведенную под построенное дерево. Переходим к
следующему тесту.
Delete(t); t = NULL;
}