3532. Интересный многоугольник
Вася нарисовал
выпуклый многоугольник с длинами последовательных сторон 1, 2, 3, …, n
(4 < n < 30), а после этого построил вокруг него окружность. Найти
радиус r окружности, описанной вокруг этого многоугольника Васей.
Вход. Количество сторон многоугольника n.
Выход. Радиус
окружности r с точностью 8 знаков после запятой.
|
Пример входа |
Пример выхода |
|
5 |
2.71756723 |
РЕШЕНИЕ
геометрия – бинарный поиск
Анализ алгоритма
Будем искать
радиус бинарным поиском. Очевидно, что r > n / 2 и r
< n2.
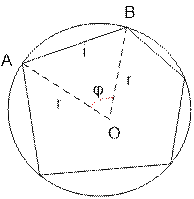
Пусть длина
стороны AB равна i. Запишем теорему косинусов для треугольника AOB:
i2 = r2
+ r2 – 2 * r * r * cosφ
Или то же самое
что и i2 = 2r2 – 2r2cosφ,
откуда cosφ = (2r2 – i2) / 2r2.
Вычислим сумму углов, стягивающих стороны многоугольника с длинами 1, 2, 3, …, n.
Если полученная сумма углов больше 2π, то радиус следует уменьшить. Иначе
радиус следует увеличить. Вычисляем значение радиуса, например, с точностью до
10-11.
Реализация алгоритма
Объявим константы.
#define EPS 1e-11
#define PI acos(-1.0)
Читаем
количество сторон n. Устанавливаем границы бинарного поиска для радиуса
описанной окружности [Left .. Right] = [n / 2 .. n2].
scanf("%d",&n);
Left = n / 2; Right = n * n;
Пока длина
отрезка [Left .. Right] не меньше 10-11, продолжаем
бинарный поиск.
while(fabs(Right - Left) > EPS)
{
Делим отрезок [Left .. Right] пополам точкой
Middle. Полагая радиус окружности равным Middle, вычисляем в
переменной fi сумму углов, стягивающих стороны многоугольника.
Middle = (Left + Right) / 2;
for(fi = 0, i = 1; i <= n; i++)
{
double angle = (2*Middle*Middle -
i*i)/(2*Middle*Middle);
Если треугольника со сторонами i, Middle, Middle
составить нельзя, то значение косинуса соответствующего угла может выходить за
пределы отрезка [-1, 1]. Следовательно необходимо уменьшать величину радиуса
описанной окружности.
if ((angle < -1.0) || (angle >
1.0))
{
fi = 100; break;
}
fi += acos(angle);
}
В зависимости от найденной суммы углов fi, корректируем
отрезок поиска.
if (fi > 2*PI) Left = Middle; else Right = Middle;
}
Выводим ответ.
printf("%.8lf\n",Left);