3532. Interesting polygon
Vasya drew a
convex polygon with sides of length 1, 2, 3, ..., n (4 ≤ n ≤ 30),
and then built the circle around it. Find the radius r of the
circle drawn around the polygon by Vasya.
Input. Number of
sides n in a polygon.
Output. Print
radius r of a circle
with 8 digits after the decimal point.
|
Sample
input |
Sample
output |
|
5 |
2.71756723 |
SOLUTION
geomentry – binary search
Algorithm analysis
We’ll search for
the radius by binary search. It's obvious that r > n / 2 and r < n2.
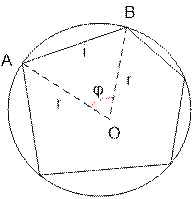
Let the length
of the side AB be equal to i. Write the cosine
theorem for triangle AOB:
i2 = r2
+ r2 – 2 * r * r * cosφ
Or the same as i2 = 2r2
– 2r2cosφ, whence cosφ = (2r2 – i2)
/ 2r2. Compute the sum of angles subtending the sides of the polygon with
lengths 1, 2, 3,…, n. If the resulting sum of angles is greater than 2π,
then the radius should be decreased. Otherwise, the radius should be increased. Find the value of
the radius, for example, with an accuracy of 10-11.
Algorithm realization
Declare the constants.
#define EPS 1e-11
#define PI acos(-1.0)
Read the number
of sides n. Set the boundaries of the binary search
for the radius of the circumscribed circle [Left .. Right] = [n
/ 2 .. n2].
scanf("%d",&n);
Left = n / 2; Right = n * n;
While the length
of the segment [Left .. Right]
is not less than 10-11, continue the binary search.
while(fabs(Right - Left) > EPS)
{
Divide the segment [Left .. Right] in half with the Middle point. Assuming the radius of the
circle to be Middle, calculate in the
variable fi the sum of the
angles that subtend the sides of
the polygon.
Middle = (Left + Right) / 2;
for(fi = 0, i = 1; i <= n; i++)
{
double angle = (2*Middle*Middle -
i*i)/(2*Middle*Middle);
If a triangle with sides i, Middle, Middle
cannot be constructed, then the
cosine value of the corresponding angle may go beyond the segment [-1, 1].
Therefore, it is necessary to reduce the value of the radius of the
circumscribed circle.
if ((angle < -1.0) || (angle >
1.0))
{
fi = 100; break;
}
fi += acos(angle);
}
Depending on the found sum of angles fi, adjust the search segment.
if (fi > 2*PI) Left = Middle; else Right = Middle;
}
Print the answer.
printf("%.8lf\n",Left);