3535.
Vasya and matrix
Mother gave Vasya a rectangular matrix n
by m. Each cell of the matrix contains one integer. Vasya played a lot
of math games with it: he found its determinant and powered it into some
degrees.
But such games made him a little tired, so
he invented a new entertainment: he chooses an integer k and tries to
find a submatrix of maximal area with total sum of numbers in it not greater
than k. The submatrix is a rectangular area of matrix.
Input. The first line contains three integers n, m and k (1 ≤ n, m ≤ 300,
1 ≤ k ≤ 109).
Each of the next n lines
contains m nonnegative integers, each no more than 1000.
Output. Print the area of maximal submatrix, which sum of
numbers is not greater than k.
|
Sample
input 1 |
Sample
output 1 |
|
1 3 4 8 6 4 |
1 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
3 3 12 7 5 7 8 4 8 4 3 2 |
3 |
SOLUTION
dynamic
programming + binary seasrch
Algorithm analysis
Let a be
the input rectangular matrix. Let’s create a two-dimensional array dp of the same size,
where dp[i][j] equals to the sum of numbers in the submatrix with opposite vertices (1, 1) and (i,
j). Its cells can be computed using the
formula:
dp[i][j]
= dp[i – 1][j] + dp[i][j – 1] – dp[i – 1][j – 1] + a[i][j]
Consider a
submatrix of array a of size w * h. Let its opposite vertices have
coordinates (i, j) and (i + w – 1, j + h – 1).
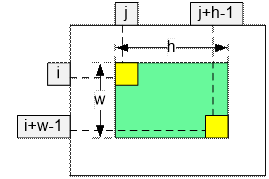
Then the sum of
all numbers in submatrix is
dp[i + w
– 1][j + h – 1] – dp[i + w – 1][j – 1] – dp[i – 1][j + h
– 1] + dp[i – 1][j – 1]
We solve the
problem using
a
brute force. Let’s enumerate all possible sizes of submatrix w * h and all possible upper left angles (i,
j) of the location of this matrix. In constant time, using the
dp array, we find the sum of numbers on this submatrix. If it does not exceed k, then among all
such submatrices we consider the maximum of their areas. However, such an
enumeration in O(n4) can
be accelerated to O(n3logn) using a binary
search over the width h of the enumerated submatrix.
Let’s fix the upper
left corner (i, j).
Let g(w, h) be the sum of numbers in the submatrix (i,
j) – (i + w – 1, j + h
– 1). If we fix w and consider h as a variable,
then g(w, h) is a non-decreasing function with
respect to h (array a
contains non-negative integers). With binary search, we find the maximum value of h for which g(w,
h) ≤ k.
Example
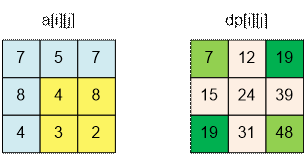
For example, the
sum of numbers in submatrix (2, 2) – (3, 3) is 48 – 19 – 19 + 7 = 17.
Algorithm realization
Store the input
matrix in the array a.
#define MAX 210
int a[MAX][MAX], dp[MAX][MAX];
Function f(w, h) returns 1 if there is a submatrix of
size w * h such that the sum of its elements is at most k. All possible upper left angles (i, j) are enumerated
and the sum of the numbers in the rectangle (i, j) – (i + w
– 1, j + h – 1) is determined using the dp array in constant time.
int f(int w, int h)
{
for (int i = 1; i + w
- 1 <= n; i ++)
for (int j = 1; j + h
- 1 <= m; j ++)
if (dp[i + w - 1][j + h - 1] - dp[i + w
- 1][j - 1] –
dp[i - 1][j + h - 1] + dp[i - 1][j - 1] <= k) return 1;
return 0;
};
The main part of the program. Read the input matrix.
scanf("%d
%d %d",&n,&m,&k);
for(i = 1; i <= n; i++)
for(j = 1; j <= m; j++)
scanf("%d",&a[i][j]);
From the input matrix a compute the matrix dp.
for (i = 1; i <= n; i++)
for (j = 1; j <= m; j++)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + a[i][j];
Iterate over the width of submatrix w.
answer = 0;
for (w = 1; w <= n; w++)
{
Iterate the length of submatrix using binary search on the interval [l;
r].
l = 1; r = m;
while (l < r)
{
mid =
(l + r) / 2;
For a submatrix of size w * mid, consider all possible top left positions (i, j). If there exists such position that the sum of the numbers in it is no more
than k, then recompute the resulting area answer.
if (f(w,mid))
{
answer = max(answer, w * mid);
l =
mid + 1;
}
else r = mid;
}
mid =
(l + r) / 2;
if (f(w,mid))
answer = max(answer, w * mid);
};
Print the area of the
found maximum submatrix.
printf("%d\n",answer);