3536. Рисовая компания

Новый украинский фермер старый дед Василий имеет в своём распоряжении прямоугольный участок n на m. Разобъем его на единичные квадратики. В каждом из них растёт сорт риса (не удивляйтесь, рис является достаточно ценным и выгодным продуктом). Для простоты сорта риса пронумерованы числами от 1 до n * m.

Совсем недавно деду Василию удалось заключить сделку с компанией IPC (International Рис Corporation) на t дней. Согласно условий этой сделки каждый день фермер должен поставлять рис определённого сорта.

Пусть у деда Василия заказали рис сорта k. Тогда он действует по следующему принципу: на участке n на m он выбирает прямоугольный участок максимальной площади, на котором ростёт только рис сорта k. То есть дед Василий собирает рис определённого сорта только с прямоугольных участков.

Для компании ІРС важно знать, какое максимальное количество риса определённого сорта сможет поставлять дед Василий для каждого запроса. Известно, что с одного единичного квадрата дед Василий получает одну условную единицу товара, то есть из участка площадью s дед Василий получает s единиц риса. Также известно, что с определённой площади дед Василий может сколько угодно раз подряд собирать рис.

Вход. В первой строке задано два целых числа n и m (1 ≤ n, m ≤ 1000) – размеры участка деда Василия. В последующих n строках задано по m целых чисел в каждой, a[i][j] – сорт риса, который растёт в j-ом квадратике і-ой строки, 1 ≤ a[i][j] ≤ n * m.

После этого задано число t (1 ≤ t ≤ 20) – количество дней, на протяжении которых дед Василий должен поставлять рис в компанию. В последующих t строках задано по одному целому числу k (1 ≤ k ≤ n * m) – сорт риса, который заказывает фирма.

Выход. Выведите t чисел – для каждого запроса компании ІРС максимальное количество риса, которое сможет собрать дед Василий.

Пример входа	Пример выхода
4 2 1 3 5 2 4 2 2 3 4 1 2 3 4	1 2 1 1

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

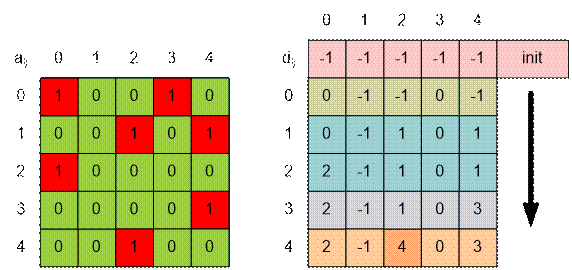
Каждый запрос обрабатываем отдельно. Пусть необходимо решить задачу для риса сорта type. Построим матрицу z, для которой z[i][j] = 0, если а[i][j] = type. Иначе положим z[i][j] = 1. Размер наибольшей нулевой подматрицы в матрице z и будет ответом на запрос.

Рассмотрим алгоритм вычисления наибольшей нулевой подматрицы.

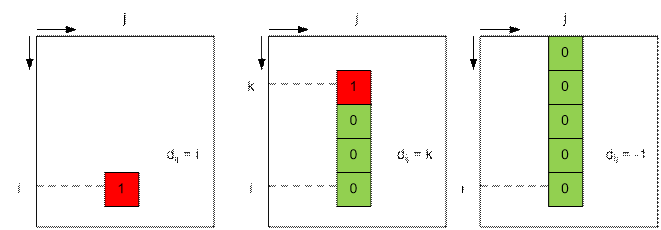
Вспомогательная динамика

Пусть d[i][j] содержит ближайшую сверху единицу для элемента a[i][j]. То есть d[i][j] содержит наибольший номер строки (среди строк в диапазоне от -1 до i), в которой в j-ом столбце стоит единица. Если такой строки нет, то d[i][j] полагается равным -1 (считаем, что вся матрица как будто ограничена снаружи единицами).

Считаем динамику двигаясь по матрице сверху вниз: пусть мы стоим в i-ой строке и известно значение динамики для предыдущей строки. Тогда достаточно скопировать эти значения в динамику для текущей строки, изменив только те элементы, в которых в матрице стоят единицы. В таком случае даже не требуется хранить всю прямоугольную матрицу динамики, а достаточно только одного массива.

Основное решение

Искомая нулевая подматрица ограничена со всех четырёх сторон единичками (либо границами поля), которые и мешают ей увеличиться в размерах и улучшить ответ. Искать подматрицу будем следующим образом: сначала переберём номер i нижней строки нулевой подматрицы, затем переберём в каком столбце j мы будем упирать вверх нулевую подматрицу. Пользуясь значением d[i][j], мы сразу получим номер верхней строки нулевой подматрицы. Остается определить оптимальные левую и правую границы нулевой подматрицы, то есть максимально раздвинуть эту подматрицу влево и вправо от j-го столбца.

Раздвинуть максимально влево означает найти такой ближайший слева к j индекс k₁, для которого d[i][k₁] > d[i][j]. В таком случае k₁ + 1 и есть номер левого столбца искомой нулевой подматрицы. Если такого индекса нет, то положм k₁ = -1 (текущая нулевая подматрица расширена влево до упора, до границы всей матрицы).

Симметрично ищем ближайший справа к j индекс k₂, для которого d[i][k₂] > d[i][j] (если такого индекса нет, то k₂ положим равным количеству столбцов. Например, если имеется n столбцов, пронумерованных от 0 до n – 1, то положим k₂ = n).

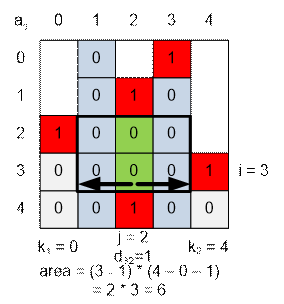
После нахождения индексов k₁ и k₂, вычисляем площадь текущей нулевой подматрицы. Она равна (i – d[i][j]) * (k₂ – k₁ – 1).

Рассмотрим процесс вычисления массива d1 на примере третьей строки:

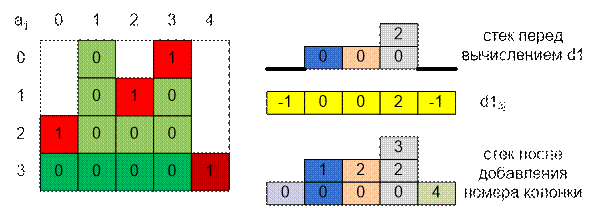
Пример

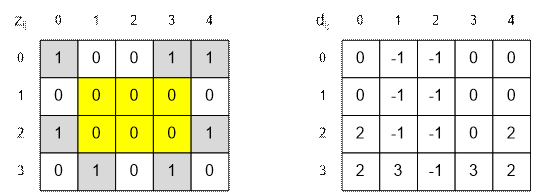
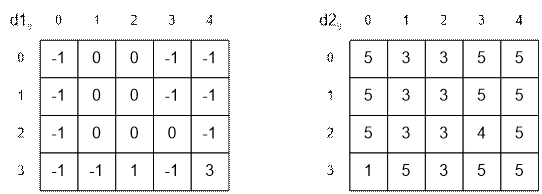
Соответствующие массивы d₁ и d₂ имеют вид:

Реализация алгоритма

#include <algorithm>

#include <stack>

#include <cstdio>

#define MAX 1009

using namespace std;

int z[MAX][MAX], d[MAX], d1[MAX], d2[MAX], a[MAX][MAX];

int main(void)

{

int n, m, i, j, t;

scanf("%d %d", &n, &m);

for(i = 0; i < n; i++)

for(j = 0; j < m; j++)

scanf("%d", &a[i][j]);

scanf("%d", &t);

while(t--)

{

int ans = 0, cur;

scanf("%d", &cur);

fill_n(d, m, -1);

fill_n(d1, m, 0);

fill_n(d2, m, 0);

stack<int> st;

for(i = 0; i < n; i++)

for(j = 0; j < m; j++)

z[i][j] = a[i][j] != cur;

for(i = 0; i < n; i++)

{

for(j = 0; j < m; j++)

if (z[i][j] == 1)

d[j] = i;

while (!st.empty())

st.pop();

for(j = 0; j < m; j++)

{

while(!st.empty() && d[st.top()] <= d[j])

st.pop();

d1[j] = st.empty() ? -1 : st.top();

st.push(j);

}

while(!st.empty())

st.pop();

for(j = m - 1; j >= 0; j--)

{

while(!st.empty() && d[st.top()] <= d[j])

st.pop();

d2[j] = st.empty() ? m : st.top();

st.push(j);

}

for(j = 0; j < m; j++)

ans = max(ans, (i - d[j]) * (d2[j] - d1[j] - 1));

}

printf("%d\n", ans);

}

}