3640. Максимальный поток
Дан
неориентированный граф без петель и кратных ребер из n вершин (вершины
нумеруются от 1 до n). Для каждого ребра известна его пропускная
способность. Найдите величину максимального потока из вершины 1 в вершину n.
По каждому ребру поток может течь в любую сторону.
Вход. Два числа n
и k (2 ≤ n ≤ 100, 0 ≤ k ≤ n
* (n - 1) / 2) – количество вершин и ребер в графе. Далее следуют k
строк по три числа в каждой – a, b, c (1 ≤ a,
b ≤ n, 1 ≤ c ≤ 109) – номера
вершин, соединенных ребром, и пропускная способность ребра.
Выход. Выведите величину максимального потока из вершины 1 в
вершину n.
|
Пример
входа |
Пример
выхода |
|
5 7 1 2 2 2 5 5 1 3 6 3 4 2 4 5 1 3 2 3 2 4 1 |
6 |
РЕШЕНИЕ
графы – максимальный поток
Анализ алгоритма
В задаче
необходимо реализовать алгоритм Диница поиска максимального паросочетания с временной
оценкой O(V2E). При реализации в этой задаче алгоритма Эдмондса –
Карпа получим Time Limit.
Пример
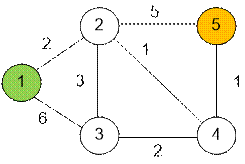
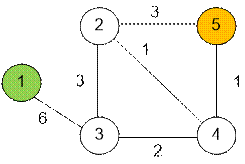
Граф, заданный в
тесте, имеет следующий вид. Исток отображен зеленым, а сток –оранжевым цветом.
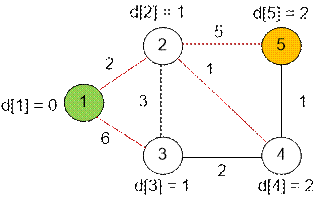
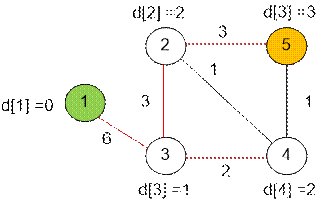
Фаза 1. Поиск в ширину. d[i]
содержит наименьшее количество ребер, которое следует пройти от истока 1, чтобы
пропасть в вершину i. Красным обозначены древесные ребра поиска в
ширину. С правой стороны представлена слоистая сеть. Она содержит те и только
те ребра (u, v), для которых d[v] = d[u] + 1.
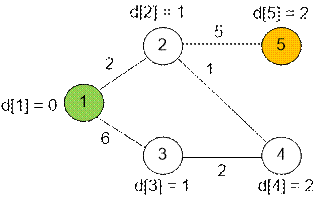
Первый запуск
поиска в глубину на слоистой сети. Синим обозначен найденный дополняющий
путь величины 2.
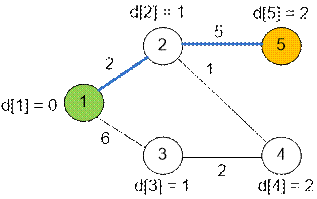
Второй запуск
поиска в глубину на слоистой сети пути между вершинами 1 и 5 не найдет.
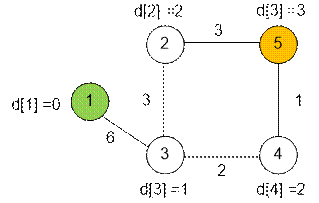
Фаза 2. Поиск в ширину.
Слоистую сеть отобразим справа.
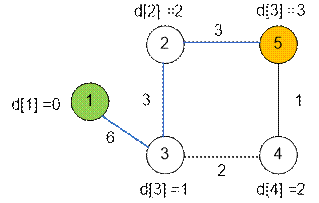
Первый запуск
поиска в глубину на слоистой сети. Синим обозначен найденный дополняющий
путь величины 3. Пропустив этот поток, получим сеть справа.
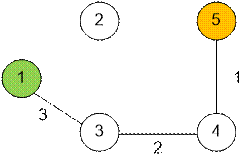
Второй запуск
поиска в глубину на слоистой сети. Синим обозначен найденный дополняющий
путь величины 1.
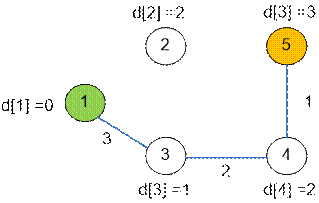
Третий запуск
поиска в глубину на слоистой сети пути между вершинами 1 и 5 не найдет.
Остаточная сеть имеет
вид:
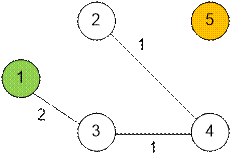
Фаза 3. Поиск в ширину.
Вершина 5 недосягаема из вершины 1 на остаточной сети. Алгоритм заканчивается.
Максимальный поток равен 6.
Реализация
алгоритма
Максимальное
количество вершин графа равно MAX. Плюс бесконечность положим равной INF.
#define MAX 101
#define INF 0x3F3F3F3F
Пропускную способность ребер храним в массиве Cap. ptr[i]
хранит номер вершины, до которой были просмотрены ребра, исходящие из вершины i
при поиске в глубину. Другими словами ptr[i] хранит указатель на последнее
ребро, по которому мы еще можем пустить увеличивающий поток. d – массив
кратчайших расстояний при поиске в ширину.
long long Cap[MAX][MAX];
int ptr[MAX], d[MAX];
Поиск в глубину
из вершины s. В массиве q
моделируется очередь при поиске в ширину. Переменная qh содержит
указатель на начало очереди, qt – на конец очереди. Заполняем ячейки d[i]
кратчайшим расстоянием от s до i. Расстояние вычисляется по
количеству ребер.
long long bfs(int s)
{
int q[MAX];
int qh = 0, qt = 0;
q[qt++] = s;
memset (d, -1, sizeof(d));
d[s] = 0;
while (qh < qt)
{
int v = q[qh++];
for (int
to = 1; to <= n; to++)
if ((d[to] == -1) && Cap[v][to])
{
q[qt++] = to;
d[to] = d[v] + 1;
}
}
return d[n] != -1;
}
Запускаем поиск
дополняющего пути из вершины v, если
известно, что величина потока от истока до v равна flow.
long long dfs(int v, long long flow)
{
if (!flow) return 0;
if (v == n) return flow;
for (int &to =
ptr[v]; to <= n; to++)
{
Двигаемся только по ребрам (v, to) слоистой сети (для которых d[to] = d[v] + 1).
if (d[to] != d[v] + 1) continue;
Если от истока до v
можно пропустить максимальный поток величины flow, то от истока до to
можно пропустить максимальный поток величины min(flow, Cap[v][to]).
int pushed = dfs (to, min (flow,
Cap[v][to]));
Если существует дополняющий путь, по которому можно увеличить
поток от v до стока на величину pushed, то меняем значение пропускной
способности ребра (v, to).
if (pushed)
{
Cap[v][to] -= pushed;
Cap[to][v] += pushed;
return pushed;
}
}
return 0;
}
Запускаем алгоритм Диница из вершины s.
long long Dinic(int s)
{
long long flow = 0;
for (;;)
{
if (!bfs(s)) break;
for(int
i = 1; i <= n; i++) ptr[i] = 1;
while (long
long pushed = dfs (s, INF))
flow += pushed;
}
return flow;
}
Основная часть
программы. Читаем входные данные, строим граф.
scanf("%d
%d",&n,&Edges);
memset(Cap,0,sizeof(Cap));
while (Edges--)
scanf("%d %d %d",&a,&b,&c),
Cap[a][b] += c, Cap[b][a] += c;
Запускаем алгоритм Диница.
MaxFlow = Dinic(1);
Выводим величину максимального потока.
printf("%lld\n",MaxFlow);
Реализация при помощи класса
class Graph
{
public:
int n;
vector<vector<long long> > Cap;
vector<int> ptr, d;
Создаем граф с n
вершинами. Вершины нумеруются числами от 1 до n.
Graph(int n = 1) : n(n)
{
Cap.assign(n+1,vector<long long>(n+1,0));
}
Добавление неориентированного ребра (From, To) с пропускной
способностью Len.
void AddNotOrientedEdge(int
From, int To, int
Len)
{
Cap[From][To] = Cap[To][From] = Len;
}
Поиск в ширину из вершины s.
long long bfs(int s)
{
int qHead = 0, qTail = 0;
int *q = new
int[n+1];
q[qTail++] = s;
d.assign(n+1,-1); d[s] = 0;
while (qHead < qTail)
{
int v = q[qHead++];
for (int
to = 1; to <= n; to++)
if ((d[to] == -1) && Cap[v][to])
{
q[qTail++] = to;
d[to] = d[v] + 1;
}
}
delete[] q;
return d[n] != -1;
}
Запускаем поиск дополняющего пути из
вершины v, если известно, что
величина потока от истока до v равна flow. Двигаемся только по
ребрам слоистой сети.
long long dfs(int v, long long flow)
{
if (!flow) return 0;
if (v == n) return flow;
for (int
&to = ptr[v]; to <= n; to++)
{
if (d[to] != d[v] + 1) continue;
long long
pushed = dfs(to, min(flow, Cap[v][to]));
if (pushed)
{
Cap[v][to] -= pushed;
Cap[to][v] += pushed;
return pushed;
}
}
return 0;
}
Реализация алгоритма Диница из вершины Start.
long long Dinic(int Start)
{
long long
flow = 0;
for (;;)
{
if (!bfs(Start)) break;
ptr.assign(n+1,1);
while (long
long pushed = dfs(Start, INF))
flow += pushed;
}
return flow;
}
};
Основная часть
программы. Читаем входные данные, строим граф.
scanf("%d
%d",&n,&Edges);
g = new
Graph(n);
while (Edges--)
{
scanf("%d %d %d",&u,&v,&Len);
g->AddNotOrientedEdge(u,v,Len);
}
Запускаем алгоритм Диница и выводим величину максимального
потока.
printf("%lld\n",g->Dinic(1));