3641. Максимальный поток B
Дан двудольный
граф, исток и сток. Каждая доля состоит из n вершин. Из истока в левую
долю ведут ребра пропускной способности ai, из каждой вершины
правой доли в сток ведут ребра пропускной способности bi.
Также есть ребра между вершинами левой и правой долей бесконечной пропускной
способности, по которым поток может течь как в одну, так и в другую сторону.
Найти величину максимального потока из истока в сток.
Вход. В первой строке
даны числа n и k (1 ≤ n ≤ 104, 0
≤ k ≤ 105) – количество вершин в каждой из долей
и количество ребер между долями. Во второй строке перечислены числа ai
(1 ≤ ai ≤ 104) – пропускные
способности ребер из истока в каждую вершину левой доли. В третьей строке
перечислены числа bi (1 ≤ bi ≤
104) – пропускные способности ребер из каждой вершины правой доли в
сток. В каждой из последующих k строк записаны по два числа u и v
(1 ≤ u, v ≤ n) означающие наличие ребра и
вершины u левой доли в вершину v правой доли.
Выход. Вывести величину максимального потока.
|
Пример
входа |
Пример
выхода |
|
3 4 3 2 1 5 4 4 1 1 1 2 2 3 3 3 |
6 |
РЕШЕНИЕ
графы – максимальное паросочетание
Анализ алгоритма
Рассмотрим граф
без ребер, исходящих из истока и входящих в сток. При помощи поиска в глубину
выделим в нем компоненты связности. Рассмотрим одну из таких компонент. Пусть в
нее входят ребра (идущие из истока) с общей пропускной способностью Left,
а выходят (идущие в сток) с общей пропускной способностью Right. Тогда
по этой компоненте можно пропустить максимум min(Left, Right)
потока. Перебираем все компоненты связности и суммируем полученные величины
потоков.
Пример
Граф, заданный в
тесте, имеет следующий вид. Исток отображен зеленым, а сток – оранжевым цветом.
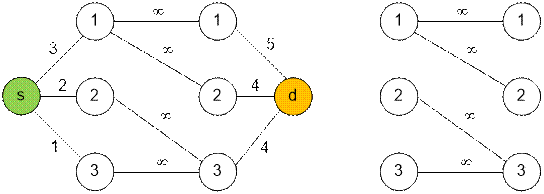
Граф без
исходящих из истока и входящих в сток ребер имеет две компоненты связности. В
первую компоненту входят ребра суммарной пропускной способности 3, а выходит 5
+ 4 = 9. Во вторую компоненту входят ребра суммарной пропускной способности 2 +
1 = 3, а выходит 4.
Величина
максимального потока равна min(3, 9) + min(3, 4) = 3 + 3 = 6.
Реализация
алгоритма
Входные
пропускные способности ai
и bi храним в
массивах a и b. Граф без исходящих из истока и входящих в сток ребер храним в
списке смежностей g.
#define MAX 10001
int a[MAX], b[MAX], used[2*MAX];
vector<vector<int>
> g;
Поиск в глубину
из вершины v. Проходим по всем вершинам одной компоненты связности. Для
каждой вершины v левой доли к переменной Left прибавляем значение
пропускной способности ребра, входящего в v. Для каждой вершины v
правой доли к переменной Right прибавляем значение пропускной
способности ребра, исходящего из v.
void dfs(int v)
{
if (v > n) Right += b[v-n]; else Left += a[v];
used[v] = 1;
for(int i = 0; i <
g[v].size(); i++)
{
int to = g[v][i];
if (!used[to]) dfs(to);
}
}
Основная часть
программы. Читаем входные данные.
scanf("%d
%d",&n,&k);
g.assign(2*n+1,vector<int>());
for(i = 1; i <= n; i++)
scanf("%d",&a[i]);
for(i = 1; i <= n; i++)
scanf("%d",&b[i]);
Строим граф, ребра которого неориентированные и имеют веса
бесконечность. Вершины левой доли нумеруем числами от 1 до n. Вершины
правой доли нумеруем числами от n + 1 до 2n.
for(i = 0; i < k; i++)
{
scanf("%d %d",&u,&v);
g[u].push_back(v+n); g[v+n].push_back(u);
}
Запускаем поиск в глубину на графе. Выделяем его компоненты
связности. Если в одну компоненту входят трубы пропускной способности Left,
а выходят с суммарной пропускной способностью Right, то через эту
компоненту можно пропустить поток величины min(Left, Right). Результирующую
величину максимального потока подсчитываем в переменной res.
res = 0;
memset(used,0,sizeof(used));
for(i = 1; i <= n; i++)
if(!used[i])
{
Left = Right = 0;
dfs(i);
res += min(Left,Right);
}
Выводим ответ.
printf("%d\n",res);