3641. Maximum flow B

The bipartite graph, source and sink are given. Each disjoint set consists of n vertices. The edges with capacities ai run from the source to the vertices of the left set, from each vertex of the right set the edges of capacity bi run to the sink. The edges also run from the vertices of the left set to the vertices of the right set of infinite capacity. The current can flow in both directions along these edges. Find the value of maximum flow from source to the sink.

Input. The numbers n and k (1 ≤ n ≤ 10⁴, 0 ≤ k ≤ 10⁵) are given – the number of vertices in each part of the graph and the number of edges between them. The second line contains the numbers a_i (1 ≤ a_i ≤ 10⁴) – the edge capacities from source to each vertex in the left set. The third line contains the numbers b_i (1 ≤ b_i ≤ 10⁴) – the edge capacities from each vertex of the right set to the sink. In each of the next k lines two numbers u and v (1 ≤ u, v ≤ n) are given – the edge connects the vertex u of the left set and the vertex v of the right set.

Output. Print the value of maximum flow.

Sample input	Sample output
3 4 3 2 1 5 4 4 1 1 1 2 2 3 3 3	6

SOLUTION

graphs – maximum matching

Algorithm analysis

Consider a graph without edges coming from the source and entering the sink. Using the depth first search, find the connected components in it. Consider one of these components. Let the edges that enter it (going from the source) has the total residual capacity Left, and the edges that exit it (going to the sink) has the total residual capacity Right. Then maximum flow of size min(Left, Right) can be run through this component. Iterate through all connected components and sum up the obtained flow values.

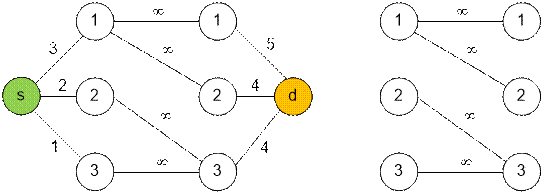
Example

Graph given in the test has the following form. The source is shown in green and the sink in orange.

The graph without edges outgoing from the source and incoming into the sink has two connected components. The first component has input edges of total capacity 3, the total capacity of output edges is 5 + 4 = 9. The second component has input edges of total capacity 2 + 1 = 3, the total capacity of output edges is 4.

The value of the maximum flow is min(3, 9) + min(3 , 4) = 3 + 3 = 6.

Algorithm realization

Input capacities a_i and b_i are stored in arrays a and b. The graph without edges outgoing from the source and entering the sink is stored in the adjacency list g.

#define MAX 10001

int a[MAX], b[MAX], used[2*MAX];

vector<vector<int> > g;

Function dfs runs the depth first search from the vertex v. Iterate over all the vertices of one connected component. For each vertex v from the left side, add to the variable Left the capacity of the edge entering v. For each vertex v from the right side, add to the variable Right the capacity of the edge outgoing from v.

void dfs(int v)

{

if (v > n) Right += b[v-n]; else Left += a[v];

used[v] = 1;

for(int i = 0; i < g[v].size(); i++)

{

int to = g[v][i];

if (!used[to]) dfs(to);

}

}

The main part of the program. Read the input data.

scanf("%d %d",&n,&k);

g.assign(2*n+1,vector<int>());

for(i = 1; i <= n; i++)

scanf("%d",&a[i]);

for(i = 1; i <= n; i++)

scanf("%d",&b[i]);

Construct a graph with undirected edges that have infinity weights. The vertices from the left part are numbered from 1 to n. The vertices from the right lobe are numbered from n + 1 to 2n.

for(i = 0; i < k; i++)

{

scanf("%d %d",&u,&v);

g[u].push_back(v+n); g[v+n].push_back(u);

}

Run the depth first search on the graph. Find its connected components. If edges with total capacity Left enter one component and exit with the total capacity Right, then a flow of min(Left, Right) can be passed through this component. The resulting value of the maximum flow is computed in the variable res.

res = 0;

memset(used,0,sizeof(used));

for(i = 1; i <= n; i++)

if(!used[i])

{

Left = Right = 0;

dfs(i);

res += min(Left,Right);

}

Print the answer.

printf("%d\n",res);