3728. Разрезание графа
Дан
неориентированный граф. Над ним в заданном порядке производятся операции
следующих двух типов:
·
cut – разрезать
граф, то есть удалить из него ребро;
·
ask – проверить,
лежат ли две вершины графа в одной компоненте связности.
Известно, что
после выполнения всех операций типа cut рёбер в графе не осталось.
Найдите результат выполнения каждой из операций типа ask.
Вход. Первая строка содержит три целых числа,
разделённых пробелами – количество вершин графа n, количество рёбер m и
количество операций k (1 ≤ n ≤ 50000, 0 ≤ m ≤ 100000, m ≤ k ≤
150000).
Следующие m строк
задают рёбра графа; i-я из этих строк
содержит два числа ui и vi (1 ≤ ui, vi ≤ n),
разделённые пробелами – номера концов i-го
ребра. Вершины нумеруются с единицы; граф не содержит кратных рёбер и петель.
Далее следует k
строк, описывающих операции. Операция типа cut задаётся строкой “cut u
v” (1 ≤ u, v ≤ n), которая означает. что из графа
удаляют ребро между вершинами u и v. Операция типа ask задаётся строкой “ask u
v” (1 ≤ u, v ≤ n), которая означает, что необходимо узнать, лежат ли в данный
момент вершины u и v в одной компоненте связности.
Гарантируется, что каждое ребро графа встретится в операциях типа cut ровно один раз.
Выход. Для каждой
операции ask во входном файле выведите в отдельной строке слово “YES”,
если две указанные вершины лежат в одной компоненте связности, и “NO” в
противном случае. Порядок ответов должен соответствовать порядку операций ask
во входном файле.
|
Пример входа |
Пример выхода |
|
3 3 7 1 2 2 3 3 1 ask 3
3 cut 1
2 ask 1
2 cut 1
3 ask 2
1 cut 2
3 ask 3
1 |
YES YES NO NO |
РЕШЕНИЕ
система непересекающихся множеств
Анализ алгоритма
Сохраним все
запросы и начнем обрабатывать их в обратном порядке. Начнем с графа, не
содержащего ребер (по условию задачи сказано, что после выполнения всех
операций типа cut множество ребер пусто). При обработке запроса “cut u
v” будем добавлять ребро между
вершинами u и v. При поступлении запроса “ask u v” будем проверять,
лежат ли вершины u и v в одной компоненте связности. Запоминание ответов на запросы ask производим в обратном порядке. После
чего выведем их в требуемом порядке.
Пример
Рассмотрим
порядок обработки запросов для приведенного примера и порядок вывода ответов на
запросы.
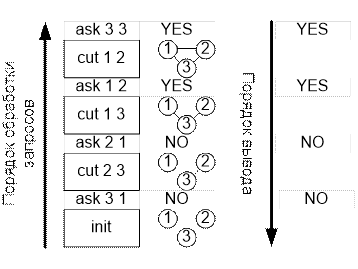
Реализация алгоритма
Операции
сохраним в массиве mas: mas[0][i] содержит 0, если i-ая операция cut и 1, если i-ая операция ask. mas[1][i] и mas[2][i] содержат
соответствующие значения u и v запросов. Массив
dsu используется при работе с системой непересекающихся множеств. res – массив
результирующих ответов.
#define MAX 150010
char op[20];
int mas[3][MAX],
dsu[MAX], res[MAX];
Функция Repr
возвращает представителя множества, которому принадлежит вершина n.
int Repr(int n)
{
if (n ==
dsu[n]) return n;
return dsu[n]
= Repr(dsu[n]);
}
Функция Union объединяет
множества, которым принадлежат вершины x
и y.
int Union(int x, int y)
{
int x1 =
Repr(x),y1 = Repr(y);
dsu[x1] = y1;
return (x1 ==
y1);
}
Основная часть
программы. Читаем значения n, m, k.
Начальное состояние графа можно пропустить.
scanf("%d %d
%d",&n,&m,&k);
for(i = 0; i
< m; i++) scanf("%d %d",&u,&v);
scanf("\n");
Входные запросы сохраняем в массиве mas.
for(i = 0; i
< k; i++)
{
scanf("%s
%d %d\n",op,&mas[1][i],&mas[2][i]);
if (op[0]
== 'a') mas[0][i] = 1; else mas[0][i] = 0;
}
Инициализируем массив dsu (вершина i указывает сама на себя).
for(i = 1; i
<= n; i++) dsu[i] = i;
Обрабатываем запросы с конца в начало. Если i-ым является запрос ask
(mas[0][i] равно 1), то занесем в
res[i] единицу при условии, что
вершины u и v находятся в одной компоненте связности (и положим res[i] = 0 иначе).
for(i = k -
1; i >= 0; i--)
{
if
(mas[0][i]) res[i] = (Repr(mas[1][i]) == Repr(mas[2][i]));
else
Union(mas[1][i],mas[2][i]);
}
Выводим ответы на последовательно поступающие запросы.
Если i-ым является запрос ask,
то выводим ответ в зависимости от значения res[i].
for(i = 0; i
< k; i++)
if
(mas[0][i])
if
(res[i]) printf("YES\n"); else printf("NO\n");