3728. Cut a graph

The undirected graph is given. Two types of operations are performed on graph in the given order:

· cut – cut a graph, or delete an edge from a graph;

· ask – check, whether two given vertices lie in the same connected component.

It is known that after performing all types of cut operations there is no edges left in the graph. Give the result for each ask operation.

Input. The first line contains three integers – the number of vertices n in a graph, the number of edges m and the number of operations k (1 ≤ n ≤ 50000, 0 ≤ m ≤ 10⁵, m ≤ k ≤ 150000).

The next m lines define the graph edges; i-th line contains two integers u_i and v_i (1 ≤ u_i, v_i ≤ n) – the end numbers of the i-th edge. The vertices are numbered starting from one; graph does not contain multiple edges and loops.

The next k lines describe the operations. Operation of type cut is given with the line “cut u v” (1 ≤ u, v ≤ n), which means that the edge between the vertices u and v is deleted from a graph. Operation of type ask is given with the line “ask u v” (1 ≤ u, v ≤ n), which means that you need to know are the vertices u and v in the same connected component. It is guaranteed that each edge of the graph meets in cut operations exactly once.

Output. For each ask operation print in a separate line the word “YES”, if two given vertices are in the same connected component, and “NO” otherwise. The order of answers must match the order of ask operations in input data.

Sample input	Sample output
3 3 7 1 2 2 3 3 1 ask 3 3 cut 1 2 ask 1 2 cut 1 3 ask 2 1 cut 2 3 ask 3 1	YES YES NO NO

SOLUTION

disjoint sets

Algorithm analysis

Save all requests and start processing them in the reverse order. Start with a graph that does not contain edges (after all cut operations are performed, the set of edges is empty). To process the request “cut u v”, we will add an edge between the vertices u and v. When the request “ask u v” arrives, we will check whether the vertices u and v lie in the same connected component. Store the answers to ask requests in the reverse order. Then print them in the required order.

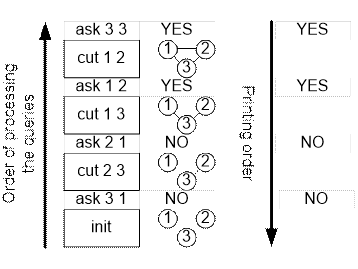
Example

Consider the order of processing the requests for the sample given and the order of printing the responses to the queries.

Algorithm realization

Save the operations in the mas array: mas[0][i] contains 0 if the i-th operation is cut and 1 if the i-th operation is ask. mas[1][i] and mas[2][i] contain the corresponding u and v query values. The dsu array is used to process a disjoint set. res is an array of resulting responses.

#define MAX 150010

char op[20];

int mas[3][MAX], dsu[MAX], res[MAX];

Function Repr returns the representative of the set that vertex n belongs to.

int Repr(int n)

{

if (n == dsu[n]) return n;

return dsu[n] = Repr(dsu[n]);

}

Function Union unites the sets to which the vertices x and y belong.

int Union(int x, int y)

{

int x1 = Repr(x),y1 = Repr(y);

dsu[x1] = y1;

return (x1 == y1);

}

The main part of the program. Read the values n, m, k. The initial state of the graph can be skipped.

scanf("%d %d %d",&n,&m,&k);

for(i = 0; i < m; i++) scanf("%d %d",&u,&v);

scanf("\n");

Store the input queries in the mas array.

for(i = 0; i < k; i++)

{

scanf("%s %d %d\n",op,&mas[1][i],&mas[2][i]);

if (op[0] == 'a') mas[0][i] = 1; else mas[0][i] = 0;

}

Initialize the dsu array (vertex i points to itself).

for(i = 1; i <= n; i++) dsu[i] = i;

Process the queries from the end to the start. If the i-th query is ask (mas[0][i] is equal to 1), then we set res[i] to one, provided that the vertices u and v are in the same connected component (and we set res[i] = 0 otherwise ).

for(i = k - 1; i >= 0; i--)

{

if (mas[0][i]) res[i] = (Repr(mas[1][i]) == Repr(mas[2][i]));

else Union(mas[1][i],mas[2][i]);

}

Print the answers to sequentially incoming queries. If the i-th query is ask, then we print the answer depending on the value of res[i].

for(i = 0; i < k; i++)

if (mas[0][i])

if (res[i]) printf("YES\n"); else printf("NO\n");