3736. Golden sand

During robbery in a store a thief found n boxes with golden sand. All the sand in a box number i has the cost v_i and the weight w_i. To carry the stolen sand, thief uses a knapsack. Find the highest total cost of sand that the robber can carry out, if knapsack capacity is limited to w.

One can pour from the boxes any amount of sand, while the ratio of the cost of the poured sand to the cost of the entire box is equal to the ratio of volume of the poured sand to the volume of entire sand box.

Input. The first line contains two integers n and w (1 ≤ n ≤ 1000, 1 ≤ w ≤ 10⁶). Each of the next n lines contains two integers. The i-th line contains the price v_i and weight w_i of the sand in the i-th box. All numbers are non-negative and do not exceed 10⁶.

Output. Print the desired maximum cost with 3 digits after the decimal point.

Sample input	Sample output
3 50 60 20 100 50 120 30	180.000

SOLUTION

greedy - knapsack

Algorithm analysis

The unit cost of sand in the i-th box is v_i / w_i. Obviously, the backpack should be loaded with as expensive sand as possible. Sort the boxes by non-increasing cost per unit of sand (non-increasing v_i / w_i). Use a greedy approach to load the knapsack.

Example

Sort the boxes of sand in nonincreasing order of the ratio v_i / w_i.

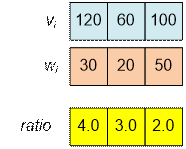
The robber can take w = 50 sand with him. He takes with him:

· 30 units of sand with total value 120;

· 20 units of sand with total value 60;

Thus, the total cost of his profit will be 180.

Algorithm realization

Declare class Sand, that contains the price of the sand price (per unit) and the weight of the available sand weight of the cost price.

class Sand

{

public:

double price;

int weight;

Sand(double price, int weight) : price(price), weight(weight) {}

};

The function f is a comparator to sort the sand. The sand is sorted in descending order of its price.

int f(Sand a, Sand b)

{

return a.price > b.price;

}

Read the input data. Store the pairs into array v: the cost of a sand unit and the weight of the sand in the box.

scanf("%d %d", &n, &w);

for (i = 0; i < n; i++)

{

scanf("%d %d", &vi, &wi);

v.push_back(Sand(1.0 * vi / wi, wi));

}

Sort the boxes in non-increasing order of sand price per unit.

sort(v.begin(), v.end(), f);

Greedily load the knapsack. The weight of the sand that can still be loaded into the knapsack is w. Take the i-th box. You can put in a backpack a weight of at most min (w, the weight of the i-th box).

for (i = 0; i < v.size(); i++)

{

res += min(w, v[i].weight) * v[i].price;

w -= min(w, v[i].weight);

}

Print the cost of sand in the knapsack.

printf("%.3lf\n", res);