3838. Частые значения

Задана последовательность n целых чисел a₁, a₂, ..., a_n в неубывающем порядке. Вам также заданы несколько запросов, состоящих из индексов i и j (1 ≤ i ≤ j ≤ n). Для каждого запроса определите число, которое чаще всего встречается среди a_i, ..., a_j.

Вход. Состоит из нескольких тестов. Каждый тест начинается со строки, содержащей два целых числа n и q (1 ≤ n, q ≤ 10⁵). Следующая строка содержит n целых чисел a₁, ..., a_n (-10⁵ ≤ a_i ≤ 10⁵). Считайте, что для каждого i Î {1, ..., n – 1}: a_i ≤ a_i+1. Каждая из следующих q строк содержит один запрос, состоящий из двух целых значений i и j (1 ≤ i ≤ j ≤ n) – границы индексов запроса.

За последним тестом следует строка, содержащая один 0.

Выход. Для каждого запроса выведите одно целое число: количество вхождений чаще всего встречаемого числа в заданном интервале.

Пример входа	Пример выхода
10 3 -1 -1 1 1 1 1 3 10 10 10 2 3 1 10 5 10 0	1 4 3

РЕШЕНИЕ

дерево отрезков

Анализ алгоритма

Заметим, что входная последовательность a_i уже отсортирована. Одинаковые элементы в ней всегда стоят рядом. Пусть T_{i, j} – количество вхождений чаще всего встречаемого числа в интервал [i, j]. Если a_i = a_j, то T_{i, j} = j – i + 1. Разобьем интервал [i, j] на два: [i, k] и [k + 1, j].

· Если a_k ≠ a_k+1, то T_{i, j} = max(T_{i, k}, T_{k+1, j});

· Если a_k = a_k+1, то T_{i, j} = max(T_{i, k}, T_{k+1, j}, количество вхождений a_k в [i, k] + количество вхождений a_k+1 в [k + 1, j]);

По последовательности а построим последовательность b такой же длины следующим образом. Пусть в последовательности а на позициях от l до r находится число x (и только на этих позициях). Тогда на позициях от l до r в последовательности b поставим числа r – l + 1. Построим дерево отрезков по последовательности b, поддерживающее максимум на отрезке.

Рассмотрим запрос (Left, Right), который возвращает количество вхождений чаще всего встречаемого числа в интервале [Left, Right].

1. Если a_Left = a_Right, то T_Left,Right = Right – Left + 1.

2. Иначе при помощи бинарного поиска найдем максимальный индекс LeftEnd, для которого a_LeftEnd = a_Left. А также найдем минимальный индекс RightBegin, для которого a_RightBegin = a_Right. Остается подсчитать, сколько раз встречаются на интервале [Left, Right] числа a_Left и a_Right. А также рекурсивно решить задачу для интервала [LeftEnd + 1, RightBegin – 1]. Среди трех полученных значений остается найти наибольшее. То есть

T_{Left, Right} = max(T_{Left, LeftEnd}, T_{RightBegin, Right}, T_{LeftEnd + 1, RightBegin – 1})

Время работы алгоритма

Построение последовательности b: O(n);

Построение дерева отрезков по последовательности b: O(n);

Время выполнения одного запроса: O(log₂n);

Итоговое время работы алгоритма: O(n + q log₂n).

Сложность по памяти: O(n)

Пример

Для последовательности а, приведенной в примере, последовательность b примет вид:

2 2 4 4 4 4 1 3 3 3

Рассмотрим запрос на интервале [Left, Right] = [5, 10].

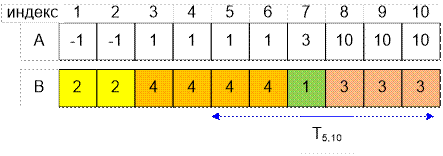
LeftEnd = 6, все элементы a_i с индексами от 5 до 6 равны 1. Таких элементов 2.

RightBegin = 8, все элементы a_i с индексами от 8 до 10 равны 10. Таких элементов 3.

Запускаем рекурсивно запрос на интервале [LeftEnd + 1, RightBegin – 1] = [7, 7]. Результатом запроса будет значение 1.

Таким образом, ответом на запрос (5, 10) будет максимум среди трех значений 2, 3 и 1.

Реализация алгоритма

Дерево отрезков храним в массиве SegmentTree длины 4*MAX, где MAX – максимальное количество элементов, которое может храниться в отрезке. Дерево будет поддерживать максимум на отрезке. Объявим также массивы a и b, которые будут хранить соответствующие последовательности.

#define MAX 100010

int SegmentTree[4*MAX];

int a[MAX], b[MAX];

Функция BuildTree строит дерево отрезков по массиву a. Ей передаются номер текущей вершины дерева Vertex и границы отрезка LeftPos и RightPos, соответствующие вершине Vertex.

void BuildTree(int *a, int Vertex, int LeftPos, int RightPos)

{

if (LeftPos == RightPos) SegmentTree[Vertex] = a[LeftPos];

else

{

int Middle = (LeftPos + RightPos) / 2;

BuildTree(a, 2*Vertex, LeftPos, Middle);

BuildTree(a, 2*Vertex+1, Middle+1, RightPos);

SegmentTree[Vertex] =

max(SegmentTree[2*Vertex],SegmentTree[2*Vertex+1]);

}

}

Функция GetMax возвращает максимум на отрезке [Left; Right]. Вершине Vertex соответствует отрезок [LeftPos; RightPos].

int GetMax(int Vertex, int LeftPos, int RightPos, int Left, int Right)

{

if (Left > Right) return -INF;

if ((Left == LeftPos) && (Right == RightPos))

return SegmentTree[Vertex];

int Middle = (LeftPos + RightPos) / 2;

return max(GetMax(2*Vertex, LeftPos, Middle, Left,

min(Right,Middle)),

GetMax(2*Vertex+1, Middle+1, RightPos,

max(Left,Middle+1),Right));

}

Основная часть программы. Читаем входную последовательность a_i в массив а.

while(scanf("%d %d",&n,&q), n)

{

for(i = 0; i < n; i++) scanf("%d",&a[i]);

По массиву a строим массив b. В переменной cnt подсчитываем количество подряд идущих одинаковых элементов.

for(bPtr = i = 0; i < n; i++)

{

cnt = 1;

while((i < n) && (a[i] == a[i+1])) cnt++, i++;

for(j = 0; j < cnt; j++) b[bPtr++] = cnt;

}

Из элементов последовательности b строим дерево отрезков, поддерживающее максимум.

memset(SegmentTree,0,sizeof(SegmentTree));

BuildTree(b,1,0,n-1);

Читаем запрос (Left, Right). Сдвигаем границы запроса на единицу влево, так как индексация массивов а и b начинается с нуля.

for(i = 0; i < q; i++)

{

scanf("%d %d",&Left,&Right);

Left--; Right--;

Если a[Left] = a[Right], то все элементы на отрезке [Left, Right] одинаковы. Возвращаем длину этого отрезка.

if (a[Left] == a[Right]) printf("%d\n",Right - Left + 1);

else

{

При помощи бинарного поиска находим максимальный индекс LeftEnd, для которого a_LeftEnd = a_Left.

int LeftEnd = (int)(upper_bound(a+Left,a+Right,a[Left]) - a) - 1;

При помощи бинарного поиска находим минимальный индекс RightBegin, для которого a_RightBegin = a_Right.

int RightBegin = (int)(lower_bound(a+Left,a+Right,a[Right]) - a);

На отрезке [Left, Right] число a_Left встречается LeftCnt раз.

int LeftCnt = LeftEnd - Left + 1;

На отрезке [Left, Right] число a_Right встречается RightCnt раз.

int RightCnt = Right - RightBegin + 1;

Решаем рекурсивно задачу для интервала [LeftEnd + 1, RightBegin – 1].

int Middle = GetMax(1,0,n-1,LeftEnd + 1, RightBegin - 1);

Среди трех полученных значений LeftCnt, RightCnt и Middle находим наибольшее и выводим ответ.

int res = max(max(LeftCnt,RightCnt),Middle);

printf("%d\n",res);

}

}

}