3838. Frequent values

You are given a sequence of n integers a₁, a₂, ..., a_n in non-decreasing order. In addition to that, you are given several queries consisting of indices i and j (1 ≤ i ≤ j ≤ n). For each query, determine the most frequent value among the integers a_i, ..., a_j.

Input. Consists of several test cases. Each test case starts with a line containing two integers n and q (1 ≤ n, q ≤ 10⁵). The next line contains n integers a₁, ..., a_n (-10⁵ ≤ a_i ≤ 10⁵). You can assume that for each i Î {1, ..., n – 1}: a_i ≤ a_i+1. The following q lines contain one query each, consisting of two integers i and j (1 ≤ i ≤ j ≤ n), which indicate the boundary indices for the query.

The last test case is followed by a line containing a single 0.

Output. For each query, print one line with one integer: the number of occurrences of the most frequent value within the given range.

Sample input	Sample output
10 3 -1 -1 1 1 1 1 3 10 10 10 2 3 1 10 5 10 0	1 4 3

SOLUTION

segment tree

Algorithm analysis

Note that the input sequence a_i is already sorted. Identical elements in it always stand side by side. Let T_{i, j} be the number of occurrences of the most frequently occurring number in the interval [i, j]. If a_i = a_j, then T_{i, j} = j – i + 1. Divide the interval [i, j] into two intervals: [i, k] and [k + 1, j].

· If a_k ≠ a_k+1, then T_{i, j} = max(T_{i, k}, T_{k+1, j});

· If a_k = a_k+1, then T_{i, j} = max(T_{i, k}, T_{k+1, j}, number of occurrences of a_k in [i, k] + number of occurrences a_k+1 in [k + 1, j]);

Given a sequence a, construct a sequence b of the same length as follows. Let the sequence a contain number x at positions from l to r (and only at these positions). Then, at positions from l to r in the sequence b, we put the numbers r – l + 1. We construct a segment tree from the sequence b, which maintains a maximum on the segment.

Consider a query (Left, Right), that returns the number of occurrences of the most frequently occurring number in the interval [Left, Right].

1. If a_Left = a_Right, then T_Left,Right = Right – Left + 1.

2. Otherwise, using binary search, find the maximum LeftEnd index for which a_LeftEnd = a_Left. And also find the minimum RightBegin index for which a_RightBegin = a_Right. It remains to count how many times occur in the interval [Left, Right] numbers a_Left and a_Right. And also recursively solve the problem for the interval [LeftEnd + 1, RightBegin – 1]. Among the three obtained values, it remains to find the largest. That is

T_{Left, Right} = max(T_{Left, LeftEnd}, T_{RightBegin, Right}, T_{LeftEnd + 1, RightBegin – 1})

Time complexity

Construct a sequence b: O(n);

Construct a segment tree by sequence b: O(n);

Time complexity of one query: O(log₂n);

The overall running time of the algorithm: O(n + q log₂n).

Memory complexity: O(n)

Example

For the sequence a given in the example, the sequence b will take the form:

2 2 4 4 4 4 1 3 3 3

Consider the query on the interval [Left, Right] = [5, 10].

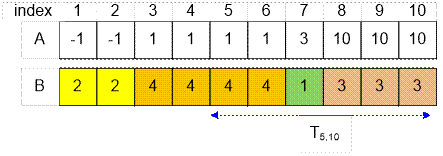
LeftEnd = 6, all elements a_i with indices from 5 to 6 are equal to 1. There are 2 such elements.

RightBegin = 8, all elements a_i with indices from 8 to 10 are equal to 10. There are 3 such elements.

Run a query recursively on the interval [LeftEnd + 1, RightBegin – 1] = [7, 7]. The result of the query will be the value 1.

Thus, the answer to the query (5, 10) will be the biggest among three values 2, 3 and 1.

Algorithm realization

The segment tree is stored in the SegmentTree array of length 4*MAX, where MAX is the maximum number of elements that can be stored in the segment. The tree will maintain a maximum on the segment. We also declare arrays a and b that will store the corresponding sequences.

#define MAX 100010

int SegmentTree[4*MAX];

int a[MAX], b[MAX];

The function BuildTree builds a segment tree from the array a. It is passed the number of the current vertex Vertex of a segment tree and the boundaries of the segment LeftPos and RightPos that correspond to the vertex Vertex.

void BuildTree(int *a, int Vertex, int LeftPos, int RightPos)

{

if (LeftPos == RightPos) SegmentTree[Vertex] = a[LeftPos];

else

{

int Middle = (LeftPos + RightPos) / 2;

BuildTree(a, 2*Vertex, LeftPos, Middle);

BuildTree(a, 2*Vertex+1, Middle+1, RightPos);

SegmentTree[Vertex] =

max(SegmentTree[2*Vertex],SegmentTree[2*Vertex+1]);

}

}

The function GetMax returns the maximum on a segment [Left; Right]. The vertex Vertex corresponds a segment [LeftPos; RightPos].

int GetMax(int Vertex, int LeftPos, int RightPos, int Left, int Right)

{

if (Left > Right) return -INF;

if ((Left == LeftPos) && (Right == RightPos))

return SegmentTree[Vertex];

int Middle = (LeftPos + RightPos) / 2;

return max(GetMax(2*Vertex, LeftPos, Middle, Left,

min(Right,Middle)),

GetMax(2*Vertex+1, Middle+1, RightPos,

max(Left,Middle+1),Right));

}

The main part of the program. Read the input sequence a_i into the array a.

while(scanf("%d %d",&n,&q), n)

{

for(i = 0; i < n; i++) scanf("%d",&a[i]);

Build array b from array a. In the variable cnt count the number of consecutive identical elements.

for(bPtr = i = 0; i < n; i++)

{

cnt = 1;

while((i < n) && (a[i] == a[i+1])) cnt++, i++;

for(j = 0; j < cnt; j++) b[bPtr++] = cnt;

}

From the elements of the sequence b build a segment tree that maintains a maximum.

memset(SegmentTree,0,sizeof(SegmentTree));

BuildTree(b,1,0,n-1);

Read a query (Left, Right). Shift the query boundaries by one to the left, since the indexing of arrays a and b starts from zero.

for(i = 0; i < q; i++)

{

scanf("%d %d",&Left,&Right);

Left--; Right--;

If a[Left] = a[Right], then all elements on the segment [Left, Right] are identical. Return the length of this segment.

if (a[Left] == a[Right]) printf("%d\n",Right - Left + 1);

else

{

Using binary search, find the maximum index LeftEnd, for which a_LeftEnd = a_Left.

int LeftEnd = (int)(upper_bound(a+Left,a+Right,a[Left]) - a) - 1;

Using binary search, find the minimum index RightBegin, for which a_RightBegin = a_Right.

int RightBegin = (int)(lower_bound(a+Left,a+Right,a[Right]) - a);

On the segment [Left, Right] number a_Left appears LeftCnt times.

int LeftCnt = LeftEnd - Left + 1;

On the segment [Left, Right] number a_Right appears RightCnt times.

int RightCnt = Right - RightBegin + 1;

Solve recursively the problem for the interval [LeftEnd + 1, RightBegin – 1].

int Middle = GetMax(1,0,n-1,LeftEnd + 1, RightBegin - 1);

Among the three obtained values LeftCnt, RightCnt и Middle find the largest and print the answer.

int res = max(max(LeftCnt,RightCnt),Middle);

printf("%d\n",res);

}

}

}