3842. Битрис
Имеется
множество 2 × n кубов. Каждому
кубу присвоено одно число от 1 до n,
это число расположено на всех его сторонах. Каждое число записано в точности на
двух кубах. Кубы расположены друг на друге, в одну стопку. Если два куба с
одинаковым числом расположены рядом, то они аннигилируют: оба куба исчезают, а
выше стоящие кубы опускаются на освободившееся место.
Ваша задача –
разобрать кучу, уничтожить
все кубики. Вам разрешается менять местами два соседних кубика. Перестановку
можно выполнять только после совершения всех возможных аннигиляций.
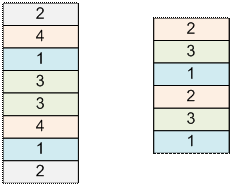
Например, если n = 4, а кубики расположены как показано
слева, то достаточно совершить один обмен. Кубики с номерами 3 аннигилируют
сразу же; Вы меняете местами четвертый снизу куб (с номером 1) с пятым снизу
кубом (с номером 4); далее кубики с номерами 4 аннигилируют, за которыми
исчезают кубики с номерами 1 и 2. Другой вариант решения задачи – поменять местами
третий и четвертый кубики снизу (в этом случае одновременно аннигилируют кубики
с номерами 1 и 4, далее исчезают кубики с номерами 2). Можно также поменять
второй и третий кубики местами.
Если n = 3, а кубики расположены как показано
справа, то необходимо совершить 3 перестановки. Одно из решений – поменять местами пятый и шестой кубики, затем
четвертый и пятый; кубики с номерами 2 аннигилируют; затем поменять местами
второй и третий; оставшиеся кубики исчезнут одновременно.
Вам необходимо
найти наименьшее количество обменов, в результате выполнения которых исчезнут
все кубики.
Вход. Первая строка содержит натуральное число n (2 ≤ n ≤ 100000). Вторая строка содержит числа, записанные на
кубах, в порядке снизу вверх.
Выход. Вывести наименьшее количество обменов, достаточное для
уничтожения всех кубиков.
|
Пример
входа |
Пример
выхода |
|
4 2 1 4 3 3 1
4 2 |
1 |
РЕШЕНИЕ
Дерево Фенвика
Анализ алгоритма
Если число val первый
раз встречается в позиции i, то
установим m[val] = i, значение a[i] увеличим на 1 (массив а моделируем Фенвиком). Когда число val встречается второй раз, уменьшаем
a[m[val]] на 1, после чего считаем
сумму чисел от m[val] до текущей
позиции i.
Пример
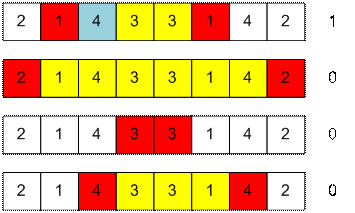
Пусть уже обработаны числа 2, 1, 4, 3 (считаем что двойка
стоит в первой позиции). Рассмотрим состояния массивов (индекс i начинается с единицы):
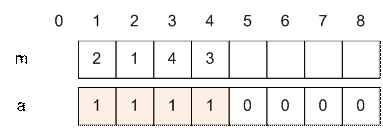
Следующее число последовательности 3, оно стоит в пятой
позиции. Уменьшаем a[m[3]] = a[4] на 1, после чего находим сумму a4
+ a5, которая равна 0 (количество чисел, стоящих между тройками,
больших 3 и встречающихся нечетное число раз).
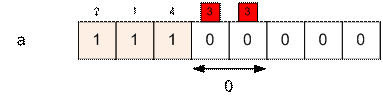
Следующее число последовательности 1, оно стоит в шестой
позиции. Уменьшаем a[m[1]] = a[2] на 1, после чего находим сумму a2
+ a3 + a4 + a5 + a6, которая равна
1 (количество чисел, стоящих между единицами, больших 1 и встречающихся
нечетное число раз).
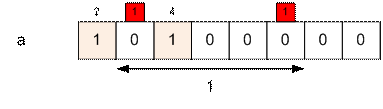
Следующее число последовательности 4, оно стоит в седьмой
позиции. Уменьшаем a[m[4]] = a[3] на 1, после чего находим сумму a3
+ a4 + a5 + a6 + a7, которая равна
0 (количество чисел, стоящих между четверками, больших 4 и встречающихся
нечетное число раз).
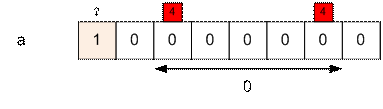
Следующее и последнее число последовательности 2, оно
стоит в восьмой позиции. Уменьшаем a[m[2]] = a[1] на 1, после чего находим
сумму a1 + … + a8, которая равна 0 (количество чисел,
стоящих между двойками, больших 2 и встречающихся нечетное число раз).

Реализация алгоритма
Реализуем дерево Фенвика Fenwick и
операции над ним. Объявим массив m.
#define MAX 200010
int Fenwick[MAX], m[MAX];
int Summma0_i(int i)
{
int result = 0;
for (; i >= 0; i = (i & (i + 1)) - 1)
result += Fenwick[i];
return result;
}
int Summmai_j(int i, int j)
{
return Summma0_i(j) - Summma0_i(i-1);
}
void IncElement(int i, int delta)
{
for (; i < MAX; i = (i | (i+1)))
Fenwick[i] += delta;
}
Основная часть программы.
scanf("%d",
&n);
memset(m,-1,sizeof(m));
res = 0;
for(i = 1; i <= 2*n; i++)
{
scanf("%d", &val);
if (m[val] == -1)
{
m[val] = i;
IncElement(i,1);
} else
{
IncElement(m[val],-1);
res += Summmai_j(m[val],i);
}
}
Выводим ответ.
printf("%lld\n",res);