3849. Дерево
Дерево
называется взвешенным, если каждому его ребру приписано одно число – длина
ребра. Все длины положительны. Для каждой вершины необходимо найти наибольшее
возможное расстояние до любой из вершин дерева.
Вход. Содержит описание дерева. Первая строка содержит количество
его вершин n (2 ≤ n ≤ 50000). Каждая из следующих n – 1 строк содержит описание ребер
дерева. Каждое ребро задается тремя положительными целыми числами. Первые два
числа – номера вершин, которые соединяет ребро, от 1 до n, третье число – длина ребра. Общая длина всех ребер не
превосходит 231 – 1. Гарантируется, что входное дерево корректно.
Выход. Выведите в точности n
строк: k-ая строка содержит
расстояние от вершины k (k = 1..n) до самой дальней вершины.
|
Пример
входа |
Пример
выхода |
|
6 1 5 3 2 6 3 6 1 1 1 3 5 4 6 4 |
5 9 10 10 8 6 |
РЕШЕНИЕ
динамическое программирование - дерево
Анализ алгоритма
depth[v] = max
(g[v][ui] + depth[ui])
Второй поиск в
глубину dfs2(v, prev, h) для каждой вершины v
будет вычислять ответ res[v]. Второй параметр
prev – предок вершины v. Значение h равно наибольшей возможной длине от v до вершины, лежащей вне поддерева с корнем v. Сначала найдем наибольшее h1
и второе наибольшее h2
расстояние от v до листа в поддереве
с корнем в v (h1 ≥ h2).
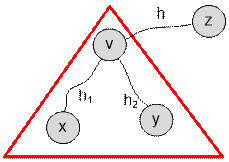
Отметим, что h1 = 
, где максимум берется по всем сыновьям to вершины v. Соответственно h2 является вторым максимум указанной суммы. Заметим также, что
значения h1 и depth[v] совпадают.
Наибольшее возможное расстояние res[v] от v до любой вершины
дерева равно
max(h, depth[v])
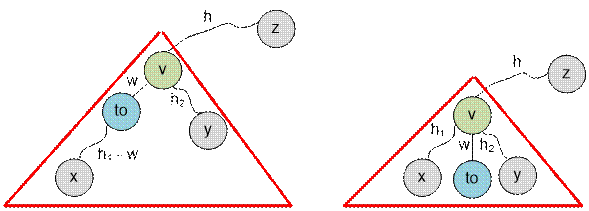
Пусть to – сын
вершины v, лежащий на пути длины h1 из v в самый дальний лист (картинка слева). Тогда при входе в to самым длинным расстоянием от to до вершины вне поддерева с корнем в to будет max(h, h2) + w, где w = g[v][to]. Поэтому состоится рекурсивный вызов
dfs2(to, v, max(h, h2) + w).
Пусть сын to
вершины v не лежит на самом длинном
пути h1 (картинка справа).
Тогда при входе в to самым длинным
расстоянием от to до вершины вне
поддерева с корнем в to будет max(h, h1)
+ w, совершаем рекурсивный вызов dfs2(to, v,
max(h, h1) + w).
Пример
Первым обходом в глубину возле
каждой вершины v вычислим значение
depth[v].
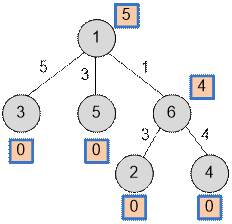
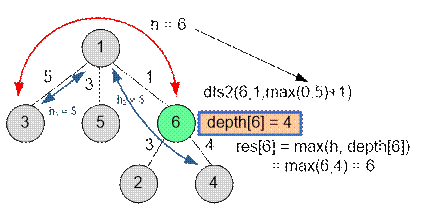
Второй обход в глубину. Для
вершины v = 1 значение h = 0, наибольшими расстояниями до
листов будут h1 = 5 и h2 = 5. При входе в вершину 6 обход в глубину будет вызван с
параметрами dfs2(6, 1, max(0, 5) + 1) или dfs2(6, 1, 6), то есть в вершине 6
значение h = 6. При первом обходе в
глубину было вычислено depth[6] = 4. Следовательно res[6] = max(h, depth[6]) = max(6, 4) = 6.
Реализация алгоритма
Взвешенное
дерево храним в списке смежностей g. Объявим рабочие массивы.
vector<vector<pair<int,int> > >
g;
vector<int> depth, res;
Максимальное
расстояние от вершины v до листа в
поддереве с корнем v вычисляем в
depth[v] при помощи функции dfs1.
void dfs1(int v, int prev = -1)
{
for(int i = 0; i <
g[v].size(); i++)
{
int to = g[v][i].first;
int w = g[v][i].second;
if(to != prev)
{
dfs1(to, v);
depth[v] = max(depth[v], depth[to] + w);
}
}
}
Второй обход в
глубину dfs2 для каждой вершины v находит наибольшее возможное расстояние до любой из вершин дерева
res[v].
void dfs2(int v, int prev = -1, int h
= 0)
{
res[v] = max(h, depth[v]);
Вычисляем наибольшее h1
и второе наибольшее h2
расстояние от v до листа в поддереве
с корнем в v.
int h1 = 0, h2 = 0;
for(int i = 0; i <
g[v].size(); i++)
{
int to = g[v][i].first;
int w = g[v][i].second;
if (to != prev)
{
int h = depth[to] + w;
if (h > h1) h2 = h1, h1 = h; else
if (h > h2) h2 = h;
}
}
for(int i = 0; i <
g[v].size(); i++)
{
int to = g[v][i].first;
int w = g[v][i].second;
if (to == prev) continue;
if(h1 == depth[to] + w)
dfs2(to,v,max(h,h2) + w);
else
dfs2(to,v,max(h,h1) + w);
}
}
Основная часть
программы. Читаем входное дерево.
scanf("%d",&n);
g.resize(n+1);
depth.resize(n+1); res.resize(n+1);
for(i = 0; i < n - 1; i++)
{
scanf("%d %d %d",&u,&v,&dist);
g[u].push_back(make_pair(v,dist));
g[v].push_back(make_pair(u,dist));
}
Совершаем два обхода в глубину.
dfs1(1);
dfs2(1);
Выводим ответ.
for(i = 1; i <= n; i++)
printf("%d\n",res[i]);