3849. Tree

 

A weighted tree is a tree where each edge is labeled with a number representing the edge’s length. All lengths are positive. For each node, you have to find the maximum possible distance to any other node in the tree.

 

Input. Contains the description of the tree. The first line contains the number of vertices n (2 ≤ n ≤ 50000) in a tree. Each of the following n – 1 lines contains the description of the tree's edges. Each edge is described by three positive integers. The first two integers are the labels of the nodes connected by this edge, ranging from 1 to n, the third number – the length of the edge. The total length of all edges does not exceed 231 – 1. It is guaranteed that the description of the tree is correct.

 

Output. Print exactly n lines: the k-th line contains the distance from node k (k = 1..n) to the most distant node.

 

Sample input

Sample output

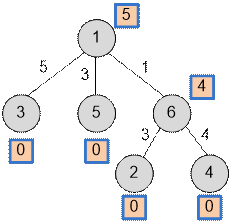
6

1 5 3

2 6 3

6 1 1

1 3 5

4 6 4

5

9

10

10

8

6

 

 

SOLUTION

dynamic programming - tree

 

Algorithm analysis

Let g[i][j] contains the weight of the edge between vertices i and j. Let’s implement the dfs1 function, which for each vertex v will find the maximum distance depth[v] from v to a leaf in the subtree rooted at v. If u1, …, uk are sons of v, and depth[ui] is already computed, then

depth[v] = max (g[v][ui] + depth[ui])

 

The second depth first search dfs2(v, prev, h) for each vertex v will compute the answer res[v]. The second parameter prev is the ancestor of the vertex v. Value of h is the maximum possible length from v to a vertex outside the subtree rooted in v. First find the largest h1 and second largest h2 distance from v to a leaf in a subtree rooted at v (h1 ≥ h2).

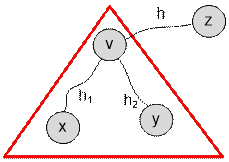
Note that h1 = , where the maximum is taken over all sons to of the vertex v. Respectively h2 is the second maximum of the indicated sum. Note also that the values of h1 and depth[v] are the same.

 

The largest possible distance res[v] from v to any vertex of the tree is

max(h, depth[v])

 

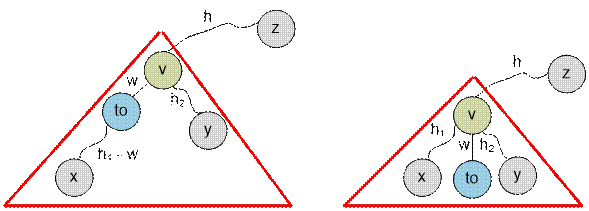
Let to be the son of the vertex v lying on the path of length h1 from v to the farthest leaf (picture on the left). Then, when entering to, the longest distance from to to a vertex outside the subtree rooted in to is max(h, h2) + w, where w = g[v][to]. Therefore, a recursive call to dfs2(to, v, max(h, h2) + w) will take place.

Let the son to of the vertex v does not lie on the longest path h1 (picture on the right). Then, when entering to, the longest distance from to to a vertex outside the subtree rooted in to will be max(h, h1) + w, we make a recursive call dfs2(to, v, max(h, h1) + w).

 

Example

With the first depth first traversal near each vertex v compute the value depth[v].

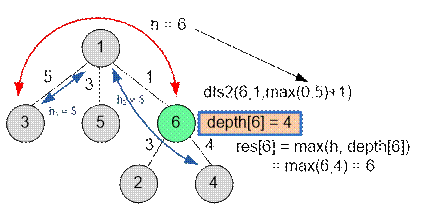
Second depth first search. For the vertex v = 1, the value h = 0, the largest distances to the leaves will be h1 = 5 and h2 = 5. When entering vertex 6, the depth first search will be called with parameters dfs2(6, 1, max(0, 5) + 1) or dfs2(6, 1, 6), that is, at the vertex 6, the value h = 6. During the first dfs, depth[6] = 4 was computed. Therefore, res[6] = max(h, depth[6]) = max(6, 4) = 6.

 

Algorithm realization

Store the weighted tree in the adjacency list g. Declare the arrays.

 

vector<vector<pair<int,int> > > g;

vector<int> depth, res;

 

The maximum distance from vertex v to a leaf in a subtree rooted in v is computed in depth[v] using the dfs1 function.

 

void dfs1(int v, int prev = -1)

{

  for(int i = 0; i < g[v].size(); i++)

  {

    int to = g[v][i].first;

    int w = g[v][i].second;

    if(to != prev)

    {

      dfs1(to, v);

      depth[v] = max(depth[v], depth[to] + w);

    }

  }

}

 

The second depth first search dfs2 for each vertex v finds the longest possible distance res[v] to any vertex of the tree.

 

void dfs2(int v, int prev = -1, int h = 0)

{

  res[v] = max(h, depth[v]); 

 

Compute the largest h1 and second largest h2 distance from v to a leaf in a subtree rooted at v.

 

  int h1 = 0, h2 = 0;

  for(int i = 0; i < g[v].size(); i++)

  {

    int to = g[v][i].first;

    int w = g[v][i].second;

    if (to != prev)

    {

      int h = depth[to] + w;

      if (h > h1) h2 = h1, h1 = h; else

      if (h > h2) h2 = h;

    }

  }

 

  for(int i = 0; i < g[v].size(); i++)

  {

    int to = g[v][i].first;

    int w = g[v][i].second;

    if (to == prev) continue;

 

    if(h1 == depth[to] + w)

      dfs2(to,v,max(h,h2) + w);

    else

      dfs2(to,v,max(h,h1) + w);

  }

}

 

The main part of the program. Read the input tree.

 

scanf("%d",&n);

g.resize(n+1);

depth.resize(n+1); res.resize(n+1);

for(i = 0; i < n - 1; i++)

{

  scanf("%d %d %d",&u,&v,&dist);

  g[u].push_back(make_pair(v,dist));

  g[v].push_back(make_pair(u,dist));

}

 

Run two depth first searches.

 

dfs1(1);

dfs2(1);

 

Print the answer.

 

for(i = 1; i <= n; i++)

  printf("%d\n",res[i]);