319. Биномиальные коэффициенты 2
Даны целые
неотрицательные числа n и k. Найти разложение биномиального
коэффициента ![]() на простые множители.
на простые множители.
Вход. Первая строка содержит количество
тестов t (t ≤ 10). Каждая из следующих t строк является отдельным тестом и содержит числа n и k
(0 ≤ n ≤ 100000, 0
≤ k ≤ n), разделенные пробелом.
Выход. Вывести
t строк, каждая из которых содержит
разложение числа ![]() на простые множители
для соответствующих входных значений.
на простые множители
для соответствующих входных значений.
Разложение
натурального числа N на простые множители следует выводить следующим образом.
Если N = 1, то необходимо вывести "1" (без кавычек), иначе пусть N = ![]() , где p1,
..., pd – все различные
простые делители числа N, упорядоченные по возрастанию, и a1, ..., ad
- натуральные числа (ai
равно максимальной степени, в которой pi
делит N). Тогда необходимо вывести строку вида
, где p1,
..., pd – все различные
простые делители числа N, упорядоченные по возрастанию, и a1, ..., ad
- натуральные числа (ai
равно максимальной степени, в которой pi
делит N). Тогда необходимо вывести строку вида
p1[^a1] * p2[^a2]
* ... * pd[^ad]
Здесь [^ai] означает, что необходимо
не писать ^ai, если ai = 1.
|
Пример входа |
Пример выхода |
|
3 1 1 4 2 6 3 |
1 2 * 3 2^2 *
5 |
РЕШЕНИЕ
комбинаторика
Анализ алгоритма
Запишем
биномиальный коэффициент в виде
![]() =
= 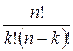 =
= ![]()
Будем
раскладывать на множители каждый из множителей, встречающийся как в числителе,
так и в знаменателе. Запоминать степени, с которыми входят в разложение ![]() простые числа, будем в
массиве deg: deg[i] ≠ 0 означает, что простое число i входит в разложение
простые числа, будем в
массиве deg: deg[i] ≠ 0 означает, что простое число i входит в разложение ![]() со степенью deg[i]. При этом для каждого простого множителя i, входящего в числитель выше приведенной дроби, будем увеличивать
deg[i] на 1. А если простой множитель
i входит в знаменатель дроби, то
будем уменьшать deg[i] на 1. Далее по
содержимому массива deg выведем разложение числа
со степенью deg[i]. При этом для каждого простого множителя i, входящего в числитель выше приведенной дроби, будем увеличивать
deg[i] на 1. А если простой множитель
i входит в знаменатель дроби, то
будем уменьшать deg[i] на 1. Далее по
содержимому массива deg выведем разложение числа ![]() на простые множители.
на простые множители.
Реализация
алгоритма
В массиве primes отмечаем простые числа решетом Эратосфена. В массиве pr сохраняем простые числа. В массив
deg заносим информацию о разложении ![]() на простые множители: deg[i] ≠ 0 означает, что i
– простое число, которое входит в разложение
на простые множители: deg[i] ≠ 0 означает, что i
– простое число, которое входит в разложение ![]() со степенью deg[i].
со степенью deg[i].
#define MAX 100010
int
primes[MAX], deg[MAX], pr[100];
Раскладываем число n на множители. Если множитель n стоит в биномиальном коэффициенте в числителе, то передаем flag = 1, если в знаменателе то flag = -1.
void
factor(int n, int
flag)
{
int i;
for(i = 0;
pr[i] <= (int)sqrt(1.0*n); i++)
while (n %
pr[i] == 0) n /= pr[i], deg[pr[i]] += flag;
if (n > 1)
deg[n] += flag;
}
Решето Эратосфена. Строим массив
primes, в котором primes[i] = 1,
только если число i простое.
void
gen_primes(void)
{
int i, j;
for(i = 0; i
< MAX; i++) primes[i] = 1;
primes[0] = primes[1] = 0;
for(i = 2; i
<= sqrt(1.0*MAX); i++)
if
(primes[i])
for(j = i
* i; j < MAX; j += i) primes[j] = 0;
Заносим в массив pr простые числа
от 2 до ![]() .
.
for(j = i =
0; i <= sqrt(1.0*MAX); i++)
if
(primes[i]) pr[j++] = i;
В конце массива ставим заглушку
(число, квадрат которого строго больше MAX).
pr[j] = MAX;
}
Моделируем вычисление
биномиального коэффициента. На самом деле раскладываем на множители все
множители, стоящие в числителе и знаменателе дроби
![]()
void
Cnk(int n, int
k)
{
int i, res =
1;
memset(deg,0,sizeof(deg));
for(i = 1; i
<= k; i++)
factor(n-i+1,1), factor(i,-1);
}
Основная часть
программы. Запускаем решето Эратосфена. Генерируем простые числа.
gen_primes();
scanf("%d",&tests);
while(tests--)
{
scanf("%d
%d",&n,&k);
if (k > n
- k) k = n - k;
if ((n == 1)
|| !k)
{
printf("1\n");
continue;
}
Вычисляем значение ![]() .
.
Cnk(n,k);
Выводим ответ. Если deg[i] ≠ 0, то простой множитель i входит в разложение ![]() со степенью deg[i].
со степенью deg[i].
for(flag = i
= 0; i < MAX; i++)
if (deg[i])
{
if(flag)
printf(" * ");
printf("%d",i);
flag = 1;
if(deg[i]
> 1) printf("^%d",deg[i]);
}
printf("\n");
}