359. Окружность и прямая
Имеется
окружность радиуса R с центром в (x, y) и прямая, заданная координатами двух
своих точек. Какой длины отрезок прямой лежит внутри окружности?
Вход. В одной строке заданы радиус окружности
R, координаты центра окружности (x, y) и координаты двух точек прямой. Все
числа целые, не превышающие 10000 по модулю.
Выход. Вывести
длину отрезка прямой внутри окружности с точностью до 5 десятичных цифр. Если
окружность и прямая не пересекаются, то вывести -1, если касаются – вывести 0.
|
Пример входа |
Пример выхода |
|
5 0 0
4 1 4 2 |
6.00000 |
РЕШЕНИЕ
геометрия
Анализ алгоритма
Уравнение
прямой, проходящей через точки (x1,
y1) и (x2, y2), имеет вид
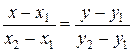 ,
,
или после
упрощения
x (y2 – y1) + y (–x2 + x1) – x1
* y2 + y1 * x2 = 0
Если уравнение имеет
вид ax + by + c = 0, то
a = y2 – y1, b = –x2 + x1, c = – x1 * y2 + y1
* x2
Расстояние от
прямой ax + by + c = 0 до центра
окружности (x0, y0) равно
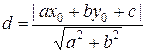
При d > r окружность и прямая не пересекаются.
При d = r окружность и прямая касаются.
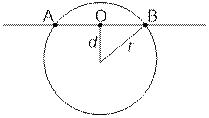
Рассмотрим
случай d < r и найдем длину отрезка AB прямой внутри окружности: AB = 2 * OB =
2 ![]() .
.
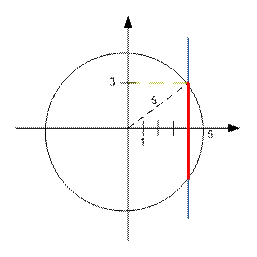
Пример
В
приведенном примере задана окружность радиусом 5 с центром (0, 0). Прямая имеет уравнение x = 4. Длина
ее части внутри окужности равна 6.
Реализация
алгоритма
Читаем входные
данные. Центр окружности имеет координаты (xx0,
yy0). Прямая проходит
через точки (xx1, yy1) и (xx2, yy2).
scanf("%d %d %d %d %d %d %d",&r,&xx0,&yy0,&xx1,&yy1,&xx2,&yy2);
Вычисляем коэффициенты a,
b и c прямой ax + by + c
= 0, проходящей через точки (xx1,
yy1) и (xx2, yy2).
a
= yy2 - yy1; b = -xx2 + xx1;
c
= -xx1*yy2 + yy1*xx2;
Вычисляем расстояние d
от центра окружности (xx0,
yy0) до прямой ax + by
+ c = 0.
d
= abs(a * xx0 + b * yy0 + c) / sqrt(1.0 * a * a + b* b);
Если d > r, то окружность и прямая не
пересекаются.
if
(d > r) printf("-1\n"); else
Если d = r, то окружность и прямая касаются.
if
(d == r) printf("0\n");
else
{
Вычисляем и выводим длину отрезка прямой внутри
окружности.
res = 2 * sqrt(1.0 * r * r - d * d);
printf("%.5lf\n",res);
}
Java
реализация
import java.util.*;
public class Main
{
public static void
main(String[] args)
{
Scanner con = new Scanner(System.in);
double r = con.nextDouble();
double x0 = con.nextDouble();
double y0 = con.nextDouble();
double x1 = con.nextDouble();
double y1 = con.nextDouble();
double x2 = con.nextDouble();
double y2 = con.nextDouble();
double a = y2 - y1;
double b = -x2 + x1;
double c = -x1 * y2 + y1 * x2; // ax + by +
c = 0
double d = Math.abs(a * x0 + b * y0 + c) / Math.sqrt(a * a + b * b);
if (d > r) System.out.println(-1); else
if (d == r) System.out.println(0); else
{
double res = 2 * Math.sqrt(r * r - d * d);
System.out.println(res);
}
con.close();
}
}