3936. Towers of Hanoi
Three pegs are
given. The first peg contains some disks in ascending order of their size from
top to bottom. The other two pegs are empty. You must move all disks from the
first peg to the second. You can move each time only one disk. It is not
allowed to put a larger disk on a smaller one.

Input. The number of
disks n (1 ≤ n ≤ 19) on the first peg.
Output. In each line
print two numbers – the peg numbers from which and where the disk is moved. The
solution must be the shortest.
|
Sample
input |
Sample
output |
|
3 |
1 2 1 3 2 3 1 2 3 1 3 2 1 2 |
SOLUTION
recursion
Algorithm analysis
Suppose we need to move n disks from the peg À to the peg B using the peg C.
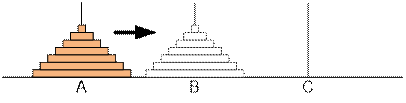
We shall use the
following recursive scheme:
·
move n – 1 disks from À to C using B;

·
move a disk from À to B;
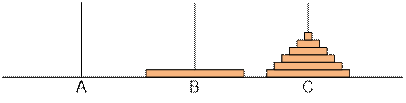
·
move n – 1 disks from C to B using À;
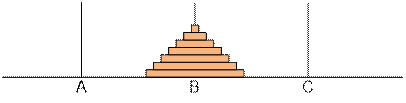
Algorithm realization
The function hanoi simulates the movement of disks from the peg from to the peg to, using an additional peg additional.
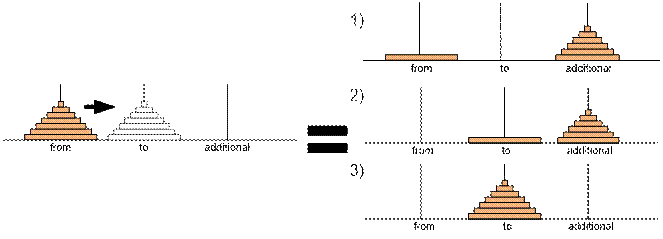
void hanoi(int
n, int from, int
to, int additional)
{
if (n == 0) return;
hanoi(n-1,from,additional,to);
printf("%d
%d\n",from,to);
hanoi(n-1,additional,to,from);
}
Read the number of disks n. Simulate the
scanf("%d",&n);
hanoi(n,1,2,3);
Java realization
import java.util.*;
public class Main
{
static void hanoi(int n, int from, int to, int additional)
{
if (n == 0) return;
hanoi(n-1,from,additional,to);
System.out.println(from + " " + to);
hanoi(n-1,additional,to,from);
}
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
hanoi(n,1,2,3);
con.close();
}
}
Python realization
def hanoi(n, fro, to, additional) :
if (n == 0) : return
hanoi(n-1,fro,additional,to)
print(fro,to)
hanoi(n-1,additional,to,fro)
n = int(input())
hanoi(n,1,2,3)