3969. Diplomas

When Peter was in school, he often participated in Olympiads in computer science, mathematics, and physics. Since he was quite capable and studied hard, he received diplomas at many of these Olympiads. By the end of school, he had accumulated n diplomas, and, as it turned out, they all had the same dimensions: w in width and h in height.

Now Peter studies at one of the best universities and lives in a hostel with his classmates. He decided to decorate his room by hanging his diplomas from school Olympiads on one of the walls. Since it is difficult to attach diplomas to a concrete wall, he decided to buy a special cork board to attach to the wall and hang diplomas on it. To make this setup look more attractive, Peter wants the board to be square and take up as little space on the wall as possible. Each diploma must be placed strictly in a w * h rectangle. Diplomas must not be rotated 90 degrees. Rectangles corresponding to different diplomas should not have common interior points.

Write a program that computes the minimum size of the square board Peter needs to accommodate all his diplomas.

Input. Three integers w, h, n (1 ≤ w, h, n ≤ 10⁹).

Output. Print the required minimum size of the square board.

Sample input	Sample output
2 3 10	9

SOLUTION

binary search

Algorithm analysis

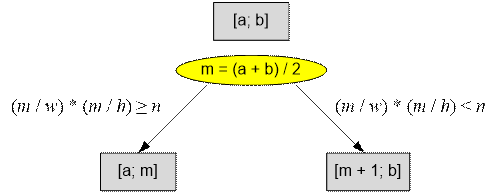
Let x be the required length of the side of the square board. Search for x using binary search. Obviously, 0 < x ≤ max(w, h) * n. Start the search in the interval [a; b] = [0; max(w, h) * n].

Let m = (a + b) / 2 be the current length of the side of the board. Since the diploma has a size of w * h, the board can accommodate a maximum of (m / w) * (m / h) diplomas. If this number is less than n, then the board size is too small, and we set a = m + 1. Otherwise, we move the right search boundary: b = m.

Let the size of the diploma is w * h = 2 * 3.

· On a 8 * 8 board, you can place a maximum of

(8 / 2) * (8 / 3) = 4 * 2 = 8 diplomas

· On a 9 * 9 board, you can place a maximum of

(9 / 2) * (9 / 3) = 4 * 3 = 12 diplomas

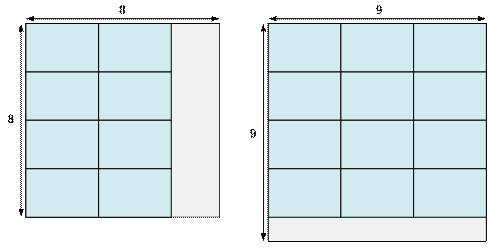
The minimum size of the board’s side, where you can place 10 diplomas, is 9.

Algorithm realization

Read the input data.

scanf("%lld %lld %lld", &w, &h, &n);

Set the boundaries of the binary search to [a; b] = [0; max(w, h) * n].

a = 0;

b = max(w, h) * n;

Start the binary search.

while (a < b)

{

m = (a + b) / 2;

The maximum number of diplomas of size w * h that can be arranged on the board with side length m is dip = (m / w) * (m / h).

dip = (m / w) * (m / h);

if (dip < n) a = m + 1;

else b = m;

}

Print the answer.

printf("%lld\n", b);

Python realization

Read the input data.

w, h, n = map(int, input().split())

Set the boundaries of the binary search to [a; b] = [0; max(w, h) * n].

a = 0

b = max(w, h) * n

Start the binary search.

while a < b:

m = (a + b) // 2

The maximum number of diplomas of size w * h that can be arranged on the board with side length m is dip = (m / w) * (m / h).

dip = (m // w) * (m // h)

if dip < n:

a = m + 1

else:

b = m

Print the answer.

print(b)