3983. Манкунианец и цветное дерево
После
напряжённой рабочей недели жители Манчестера и Ливерпуля решили отправиться в
поход на выходные. Прогуливаясь по лесу, они наткнулись на уникальное дерево,
состоящее из n вершин. Вершины дерева пронумерованы от 1 до n, и
каждая из них окрашена в один из c возможных цветов.
Чтобы побороть
скуку, они решили проверить свои логические способности. Корнем дерева является
вершина 1. Для каждой вершины участники решили найти ближайшего предка, цвет
которого совпадает с цветом этой вершины.
Вход. Первая строка
содержит два целых числа n и c (1 ≤ n, c ≤ 105)
– количество вершин в дереве и количество возможных цветов.
Вторая строка
содержит n – 1 целых чисел: i-ое из них указывает на родителя вершины i + 1.
Третья строка
содержит n целых чисел – цвета вершин. Каждый цвет лежит в
диапазоне от 1 до c включительно.
Выход. Выведите в одной строке n
чисел: для каждой вершины выведите номер её ближайшего предка с таким же
цветом. Если такого предка не существует, выведите -1.
|
Пример
входа |
Пример
выхода |
|
5 4 1 1 3 3 1 4 2 1 2 |
-1 -1 -1 1 3 |
РЕШЕНИЕ
графы –
поиск в глубину
Анализ алгоритма
Рассмотрим упрощённый
вариант задачи. Пусть все вершины дерева окрашены в один цвет. Объявим стек,
который изначально пуст. Запустим обход в глубину из корня дерева. При входе в
вершину v добавим её в стек, а при завершении обработки вершины v
удалим верхний элемент стека (им как раз и будет вершина v). После
завершения обхода стек вновь станет пустым.
Вопрос: что будет находиться на вершине стека в момент входа в вершину v,
до того как мы поместим v в стек?
Теперь перейдём к решению
исходной задачи. Создадим c стеков – по одному для каждого цвета
(например, можно использовать вектор стеков). Изначально все стеки пусты.
Запустим обход в глубину из корня дерева – вершины 1. Обработка вершины v,
окрашенной в цвет color, включает следующие шаги:
·
Если стек s[color]
не пуст, то на его вершине находится номер вершины, которая является ближайшим предком
вершины v того же цвета. Если стек пуст, то такой вершины не существует,
и в качестве ответа для вершины v следует вывести -1.
·
Добавляем вершину v
в стек s[color].
·
Рекурсивно запускаем поиск в глубину от всех сыновей
вершины v.
·
После завершения обработки удаляем вершину v из стека s[color].
Во время обхода в глубину,
находясь в вершине v, в стеках содержится информация о цветах всех
вершин, расположенных на единственном пути от корня дерева до вершины v.
В частности, стек s[color] хранит номера вершин на этом пути, окрашенных
в цвет color. Эти вершины заносятся в стек в порядке их посещения при
обходе в глубину.
Пример
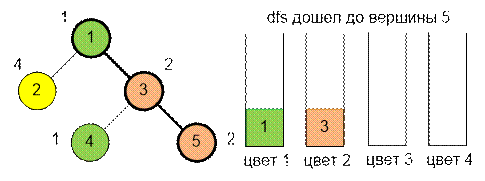
Когда поиск в
глубину дойдет до вершины 5, из c = 4
стеков два будут пустыми (соответствующие цветам 3 и 4).
Стек номер 1 (для
цвета 1) будет содержать вершину 1, стек номер 2 (для цвета 2) будет содержать
вершину 3. Так
как вершина 5 имеет цвет 2, её ближайший предок с таким же цветом находится на
вершине стека номер 2.
Таким образом, ближайшим
предком вершины 5 по цвету является вершина 3.
Реализация алгоритма
Объявим рабочие
массивы.
vector<int> col, res;
vector<vector<int> > g;
vector<stack<int> > s;
Функция dfs выполняет поиск в глубину, начиная с вершины v.
void dfs(int
v)
{
Вершина v имеет цвет color.
int color =
col[v];
Номер ближайшего предка вершины v, имеющей цвет color, сохраняем в res[v].
if(s[color].empty())
res[v] = -1;
else
res[v] = s[color].top();
Заносим вершину v в стек номер color.
s[color].push(v);
Перебираем всех сыновей to вершины v и рекурсивно запускаем из них
поиск в глубину.
for (int to : g[v])
dfs(to);
После завершения обработки вершины v (то есть при
выходе) удаляем её из стека с номером color.
s[color].pop();
}
Основная часть программы. Читаем входные данные. Строим дерево.
scanf("%d %d", &n, &c);
g.resize(n + 1);
for(i = 2; i <= n; i++)
{
scanf("%d",&val);
g[val].push_back(i);
}
Читаем цвета вершин дерева.
col.resize(n + 1);
for(i = 1; i <= n; i++)
scanf("%d",&col[i]);
Запускаем поиск в глубину из вершины 1.
s.resize(c + 1);
res.resize(n + 1);
dfs(1);
Выводим ответ.
for(i = 1; i <= n; i++)
printf("%d
",res[i]);
printf("\n");
Python реализация
import sys
sys.setrecursionlimit(1000000)
Функция dfs выполняет поиск в глубину, начиная с вершины v.
def dfs(v):
Вершина v имеет цвет color.
color = col[v]
Номер ближайшего предка вершины v, имеющей цвет color, сохраняем в res[v].
if not s[color]:
res[v] = -1
else:
res[v] = s[color][-1]
Заносим вершину v в стек номер color.
s[color].append(v)
Перебираем всех сыновей to вершины v и рекурсивно запускаем из них
поиск в глубину.
for to in g[v]:
dfs(to)
После завершения обработки вершины v (то есть при
выходе) удаляем её из стека с номером color.
s[color].pop()
Основная часть программы. Читаем входные данные. Строим дерево.
n, c = map(int, input().split())
lst = list(map(int, input().split()))
g = [[] for _ in
range(n + 1)]
for i in range(2, n + 1):
val = lst[i - 2]
g[val].append(i)
Читаем цвета вершин дерева.
col = [0] * (n + 1)
col[1:] = list(map(int, input().split()))
Запускаем поиск в глубину из вершины 1.
s = [[] for _ in
range(c + 1)]
res = [0] * (n + 1)
dfs(1)
Выводим ответ.
print(*res[1:])