3983. Mancunian and colored tree
After a long and busy work week, the residents of Manchester
and Liverpool decided to go hiking for the weekend. While walking through the
forest, they came across a unique tree consisting of n vertices. The
vertices of the tree are numbered from 1 to n, and each one is painted
in one of c possible colors.
To fight off boredom, they decided to test their logical
thinking. The root of the tree is vertex 1. For each vertex, the participants
decided to find its nearest ancestor that shares the same color.
Input.
The first line contains two integers n and c (1 ≤ n,
c ≤ 105) – the number of vertices in the tree and the
number of possible colors.
The
second line contains n – 1 integers: the i-th of them indicates the parent
of vertex i + 1.
The
third line contains n integers – the colors of the vertices. Each color
is an integer from 1 to c, inclusive.
Output.
Print n integers in a single line: for each vertex, print the number of
its nearest ancestor with the same color. If no such ancestor exists, print -1.
|
Sample
input |
Sample
output |
|
5 4 1 1 3 3 1 4 2 1 2 |
-1 -1 -1 1 3 |
SOLUTION
graphs, depth first search
Algorithm analysis
Let us consider a
simplified version of the problem. Suppose all the vertices of the tree are
painted the same color. We initialize an empty stack and perform a depth-first
search starting from the root of the tree. When entering a vertex v,
push it onto the stack. When the processing of vertex v is complete,
remove the top element from the stack (which will be vertex v itself).
After the DFS is finished, the stack will once again be empty.
Question: What will be on
the top of the stack at the moment we enter vertex v, just before we
push v onto the stack?
Now let us move
on to solving the original problem. We create c stacks – one for each
color (for example, using a vector of stacks). Initially, all stacks are empty.
Perform a DFS
starting from the root of the tree – vertex 1. The processing of a vertex v, painted in
color color, includes the following steps:
·
If the stack s[color] is not empty, its top element contains
the number of the vertex that is the nearest ancestor of vertex v with the same color. If the stack is empty, such a vertex
does not exist, and the answer for vertex v should be -1.
·
Push vertex v onto the stack s[color].
·
Recursively perform a depth-first search from all children of
vertex v.
·
After finishing the processing of vertex v, remove it
from the stack s[color].
During the depth-first search,
when we are at vertex v, the stacks contain information about the colors
of all vertices along the unique path from the root to vertex v. In
particular, the stack s[color] stores the numbers of all vertices on
this path that are colored with color. These vertices are pushed onto
the stack in the order they are visited during the DFS.
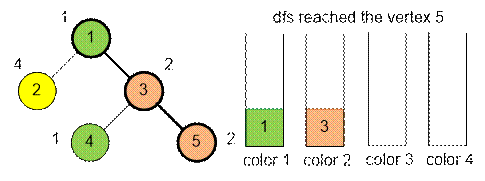
Example
When the depth-first
search reaches vertex 5, two out of the c = 4 stacks will be empty
(those corresponding to colors 3 and 4).
Stack number 1 (for color
1) will contain vertex 1, and stack number 2 (for color 2) will contain vertex
3. Since vertex 5 has color 2, its nearest ancestor with the same color is at
the top of stack number 2.
Therefore, the nearest
ancestor of vertex 5 with the same color is vertex 3.
Algorithm implementation
Declare the arrays.
vector<int> col, res;
vector<vector<int> > g;
vector<stack<int> > s;
The dfs function performs a depth-first search starting from vertex
v.
void dfs(int
v)
{
Vertex v has color color.
int color =
col[v];
The number of the nearest ancestor of vertex v with the same color
is stored in res[v].
if(s[color].empty())
res[v] = -1;
else
res[v] = s[color].top();
Push vertex v onto the stack corresponding to its color.
s[color].push(v);
Iterate over all children to of vertex v and recursively
perform a depth-first search from each of them.
for (int to : g[v])
dfs(to);
After processing vertex v is complete (i.e., upon exiting it),
remove it from the stack corresponding to its color.
s[color].pop();
}
The main part of the program. Read the input data. Construct a tree.
scanf("%d %d",&n,&c);
g.resize(n+1);
for(i = 2; i <= n; i++)
{
scanf("%d",&val);
g[val].push_back(i);
}
Read the colors of the tree’s vertices.
col.resize(n+1);
for(i = 1; i <= n; i++)
scanf("%d",&col[i]);
Start a depth first search from vertex 1.
s.resize(c+1);
res.resize(n+1);
dfs(1);
Print the answer.
for(i = 1; i <= n; i++)
printf("%d
",res[i]);
printf("\n");
Python implementation
Increase the recursion stack size.
import sys
sys.setrecursionlimit(1000000)
The dfs function performs a depth-first search starting from vertex
v.
def dfs(v):
Vertex v has color color.
color = col[v]
The number of the nearest ancestor of vertex v with the same color
is stored in res[v].
if not s[color]:
res[v] = -1
else:
res[v] = s[color][-1]
Push vertex v onto the stack corresponding to its color.
s[color].append(v)
Iterate over all children to of vertex v and recursively
perform a depth-first search from each of them.
for to in g[v]:
dfs(to)
After processing vertex v is complete (i.e., upon exiting it),
remove it from the stack corresponding to its color.
s[color].pop()
The main part of the program. Read the input data. Construct a tree.
n, c = map(int, input().split())
lst = list(map(int, input().split()))
g = [[] for _ in
range(n + 1)]
for i in range(2, n + 1):
val = lst[i - 2]
g[val].append(i)
Read the colors of the tree’s vertices.
col = [0] * (n + 1)
col[1:] = list(map(int, input().split()))
Start a depth first search from vertex 1.
s = [[] for _ in
range(c + 1)]
res = [0] * (n + 1)
dfs(1)
Print the answer.
print(*res[1:])