3984 . Сумма квадратов на дереве отрезков
Деревья отрезков
— чрезвычайно полезная структура данных. Например, с использованием ленивого
проталкивания (lazy propagation) можно эффективно выполнять операции:
вычисление суммы на отрезке за O(log n) и обновление на отрезке за O(log n).
В этой задаче
вам предстоит вычислять сумму квадратов на заданном отрезке, при этом
поддерживая два типа модификаций:
·
прибавление заданного значения ко всем элементам на
отрезке,
·
присваивание заданного значения всем элементам на отрезке.
Вход. Первая строка
содержит количество тестов.
Первая строка
каждого теста содержит два целых числа n (1 ≤ n ≤ 105) и q (1 ≤ q ≤ 105).
Следующая строка
содержит n целых чисел, каждое из которых по модулю не превышает 1000. Далее следуют q строк,
каждая из которых описывает одну операцию:
·
2 st nd – выведите сумму квадратов элементов с
индексами от st до nd (1 ≤ st ≤ nd ≤ n) включительно,
·
1 st nd x – прибавить значение x ко
всем элементам отрезка [st, nd] (1 ≤ st ≤ nd ≤ n, -1000 ≤ x ≤ 1000),
·
0 st nd x – присвоить
значение x всем элементам отрезка [st, nd] (1 ≤ st ≤ nd ≤ n, -1000 ≤ x ≤ 1000).
Выход. Для каждого
теста в первой строке выведите “Case <caseno>:”. Затем для каждой операции типа 2 выведите значение суммы квадратов на соответствующем отрезке.
Чтобы избежать
переполнения, используйте 64-битный знаковый целочисленный тип данных.
|
Пример
входа |
Пример
выхода |
|
2 4 5 1 2 3 4 2 1 4 0 3 4 1 2 1 4 1 3 4 1 2 1 4 1 1 1 2 1 1 |
Case 1: 30 7 13 Case 2: 1 |
РЕШЕНИЕ
структуры данных – дерево
отрезков
Анализ алгоритма
В задаче следует
реализовать две множественные операции: сложение и присваивание. В каждой
вершине дерева отрезков объявим тип последней выполненной операции type и параметр отложенной операции add (это будет добавляемое значение в
случае type = ADD и присваиваемое
значение в случае type = SET). И соответственно при
проталкивании (операции push) обрабатываем их отдельно. Еше следует реализовать
поддержку суммы квадратов на отрезке.
Рассмотрим отрезок [i; j]
с числами ai, …, aj. Пусть ко всем числам
отрезка добавлено число v. Сумма на
отрезке увеличится на (j – i + 1) * v. Рассмотрим на сколько увеличится сумма квадратов на отрезке.
После увеличения чисел на v квадраты
на отрезке станут равными (ai
+ v)2, (ai+1 + v)2, …, (aj + v)2.
Их сумма равна (
+ 
+ … + 
) + 2 * v * (ai + …+ aj) + (j – i
+ 1) * v2. То есть при
добавлении v ко всем числам отрезка к
текущей сумме квадратов следует добавить 2 * v * (сумма чисел на отрезке) +
(j – i + 1) * v2. Поэтому
вместе с поддержкой
суммы квадратов на отрезке следует также поддерживать и сумму на отрезке.
Проталкивание в
случае присваивания (? означает произвольное значение):
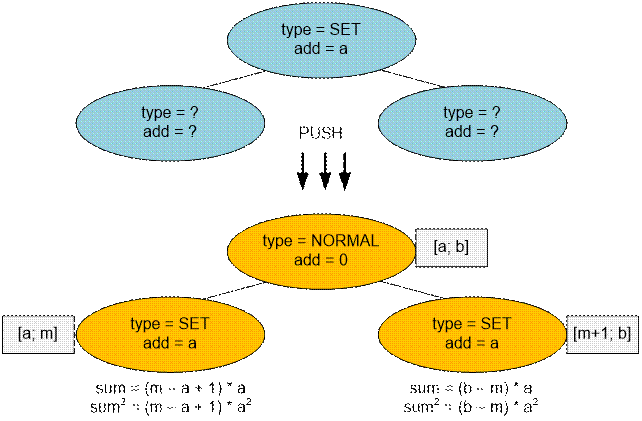
Проталкивание в
случае прибавления. Отдельно следует рассмотреть случаи когда в сыновьях
находятся различные типы отложенных операций. Если сын содержит отложенную
операцию SET или ADD, то ее тип
сохраняется после проталкивания. Если сын содержит
При пересчете в сыновьях
сначала следует обновить сумму квадратов (она использует прежнее значение суммы
на отрезке), а затем обновить и саму сумму.
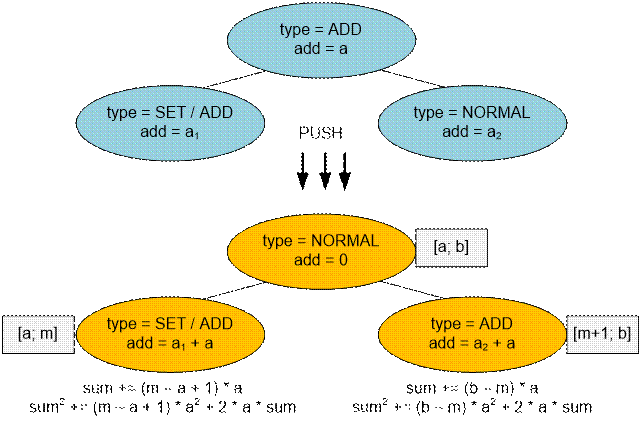
Реализация алгоритма
Следует
реализовать два типа множественных операций: прибавление (type = ADD) и присваивание (type
= SET) на отрезке.
#include <cstdio>
#include <algorithm>
#define MAX 100010
#define
#define ADD 1
#define SET 2
using namespace std;
struct node
{
long long sum, sumSq,
type, add;
} SegTree[4*MAX];
long long mas[MAX];
По массиву а строим дерево отрезков, поддерживающее сумму и
сумму квадратов на отрезке. Тип отложенной операции изначально считается
неустановленным (type = NORMAL = 0).
void build(long long *a, int Vertex, int Left,
int Right)
{
SegTree[Vertex].type = NORMAL;
SegTree[Vertex].add = 0;
if (Left == Right)
{
SegTree[Vertex].sum = a[Left];
SegTree[Vertex].sumSq = 1LL * a[Left] * a[Left];
}
else
{
int Middle = (Left + Right) / 2;
build
(a, 2*Vertex, Left, Middle);
build
(a, 2*Vertex+1, Middle+1, Right);
SegTree[Vertex].sum = SegTree[2*Vertex].sum + SegTree[2*Vertex+1].sum;
SegTree[Vertex].sumSq =
SegTree[2*Vertex].sumSq + SegTree[2*Vertex+1].sumSq;
}
}
void Push(int Vertex, int
LeftPos, int Middle, int
RightPos)
{
if (SegTree[Vertex].type == SET)
{
SegTree[2*Vertex].type = SegTree[2*Vertex+1].type =
SegTree[Vertex].type;
SegTree[2*Vertex].add = SegTree[2*Vertex+1].add = SegTree[Vertex].add;
SegTree[2*Vertex].sum = (Middle - LeftPos + 1) * SegTree[Vertex].add;
SegTree[2*Vertex].sumSq = (Middle - LeftPos + 1) *
SegTree[Vertex].add * SegTree[Vertex].add;
SegTree[2*Vertex+1].sum = (RightPos - Middle) * SegTree[Vertex].add;
SegTree[2*Vertex+1].sumSq = (RightPos - Middle) *
SegTree[Vertex].add * SegTree[Vertex].add;
SegTree[Vertex].add = 0;
SegTree[Vertex].type = NORMAL;
}
if (SegTree[Vertex].type == ADD)
{
SegTree[2*Vertex].add += SegTree[Vertex].add;
SegTree[2*Vertex].sumSq += (Middle - LeftPos + 1) *
SegTree[Vertex].add * SegTree[Vertex].add +
2LL * SegTree[Vertex].add * SegTree[2*Vertex].sum;
SegTree[2*Vertex].sum += (Middle - LeftPos + 1) * SegTree[Vertex].add;
if (SegTree[2*Vertex].type ==
if (SegTree[2*Vertex+1].type ==
SegTree[2*Vertex+1].add += SegTree[Vertex].add;
SegTree[2*Vertex+1].sumSq += (RightPos - Middle) *
SegTree[Vertex].add *
SegTree[Vertex].add +
2LL *
SegTree[Vertex].add * SegTree[2*Vertex+1].sum;
SegTree[2*Vertex+1].sum += (RightPos - Middle) * SegTree[Vertex].add;
SegTree[Vertex].add = 0;
SegTree[Vertex].type = NORMAL;
}
}
void SetValue(int Vertex, int
LeftPos, int RightPos, int
Left,
int Right, int
Value)
{
if (Left > Right) return;
if ((LeftPos == Left) && (RightPos == Right))
{
SegTree[Vertex].add = Value;
SegTree[Vertex].type = SET;
SegTree[Vertex].sum = (long long)(Right - Left + 1) * Value;
SegTree[Vertex].sumSq = (long long)(Right - Left + 1) * Value * Value;
return;
}
int Middle = (LeftPos + RightPos) / 2;
Push(Vertex,LeftPos,Middle,RightPos);
SetValue(2*Vertex, LeftPos, Middle, Left, min(Middle,Right), Value);
SetValue(2*Vertex+1, Middle+1, RightPos, max(Left,Middle+1), Right,
Value);
SegTree[Vertex].sum = SegTree[2*Vertex].sum + SegTree[2*Vertex+1].sum;
SegTree[Vertex].sumSq =
SegTree[2*Vertex].sumSq + SegTree[2*Vertex+1].sumSq;
}
void AddValue(int Vertex, int
LeftPos, int RightPos,
int Left, int
Right, int Value)
{
if (Left > Right) return;
if ((LeftPos == Left) && (RightPos == Right))
{
SegTree[Vertex].add += Value;
if (SegTree[Vertex].type ==
SegTree[Vertex].sumSq += (long long)(Right - Left + 1) * Value * Value +
2LL * Value *
SegTree[Vertex].sum;
SegTree[Vertex].sum += (long long)(Right - Left + 1) * Value;
return;
}
int Middle = (LeftPos + RightPos) / 2;
Push(Vertex,LeftPos,Middle,RightPos);
AddValue(2*Vertex, LeftPos, Middle, Left, min(Middle,Right), Value);
AddValue(2*Vertex+1, Middle+1, RightPos, max(Left,Middle+1), Right,
Value);
SegTree[Vertex].sum = SegTree[2*Vertex].sum + SegTree[2*Vertex+1].sum;
SegTree[Vertex].sumSq =
SegTree[2*Vertex].sumSq + SegTree[2*Vertex+1].sumSq;
}
long long SumSq(int
Vertex, int LeftPos, int
RightPos, int Left, int
Right)
{
if (Left > Right) return
0;
if ((LeftPos == Left) && (RightPos == Right))
return SegTree[Vertex].sumSq;
int Middle = (LeftPos + RightPos) / 2;
Push(Vertex,LeftPos,Middle,RightPos);
return SumSq(2*Vertex, LeftPos, Middle, Left,
min(Middle,Right)) +
SumSq(2*Vertex+1, Middle+1, RightPos, max(Left,Middle+1), Right);
}
int i, n, q,
cs, tests, type, l, r, x;
int main(void)
{
scanf("%d",&tests);
for(cs = 1; cs <= tests; cs++)
{
scanf("%d %d",&n,&q);
for(i = 1; i <= n; i++)
scanf("%lld",&mas[i]);
build(mas,1,1,n);
printf("Case %d:\n",cs);
while(q--)
{
scanf("%d",&type);
if (type == 0)
{
scanf("%d %d %d",&l,&r,&x);
SetValue(1,1,n,l,r,x);
} else
if (type == 1)
{
scanf("%d %d %d",&l,&r,&x);
AddValue(1,1,n,l,r,x);
} else
{
scanf("%d
%d",&l,&r);
printf("%lld\n",SumSq(1,1,n,l,r));
}
}
}
return 0;
}
Реализация алгоритма – второй вариант
В каждой вершине дерева отрезков объявим две переменные add и set для хранения информации по отложенным операциям.
#include <cstdio>
#include <algorithm>
#define MAX 100010
#define INF
2100000000
using namespace std;
struct node
{
long long sum, sumSq,
add, set;
} SegTree[4*MAX];
long long mas[MAX];
void build(long long *a, int Vertex, int Left,
int Right)
{
if (Left == Right)
{
SegTree[Vertex].sum = a[Left];
SegTree[Vertex].sumSq = 1LL * a[Left] * a[Left];
SegTree[Vertex].add = 0;
SegTree[Vertex].set = INF;
}
else
{
int Middle = (Left + Right) / 2;
build
(a, 2*Vertex, Left, Middle);
build
(a, 2*Vertex+1, Middle+1, Right);
SegTree[Vertex].sum = SegTree[2*Vertex].sum + SegTree[2*Vertex+1].sum;
SegTree[Vertex].sumSq =
SegTree[2*Vertex].sumSq + SegTree[2*Vertex+1].sumSq;
SegTree[Vertex].add = 0;
SegTree[Vertex].set = INF;
}
}
void Push(int Vertex, int
LeftPos, int Middle, int
RightPos)
{
if (SegTree[Vertex].set != INF)
{
SegTree[2*Vertex].set = SegTree[Vertex].set;
SegTree[2*Vertex].add = 0;
SegTree[2*Vertex].sum = (Middle - LeftPos + 1) * SegTree[Vertex].set;
SegTree[2*Vertex].sumSq =
(Middle - LeftPos + 1) * SegTree[Vertex].set * SegTree[Vertex].set;
SegTree[2*Vertex+1].set = SegTree[Vertex].set;
SegTree[2*Vertex+1].add = 0;
SegTree[2*Vertex+1].sum = (RightPos - Middle) * SegTree[Vertex].set;
SegTree[2*Vertex+1].sumSq = (RightPos - Middle) *
SegTree[Vertex].set * SegTree[Vertex].set;
SegTree[Vertex].set = INF;
}
if (SegTree[Vertex].add != 0)
{
SegTree[2*Vertex].add += SegTree[Vertex].add;
SegTree[2*Vertex].sumSq += (Middle - LeftPos + 1) * SegTree[Vertex].add
*
SegTree[Vertex].add +
2LL *
SegTree[Vertex].add * SegTree[2*Vertex].sum;
SegTree[2*Vertex].sum += (Middle - LeftPos + 1) * SegTree[Vertex].add;
SegTree[2*Vertex+1].add += SegTree[Vertex].add;
SegTree[2*Vertex+1].sumSq += (RightPos - Middle) *
SegTree[Vertex].add *
SegTree[Vertex].add +
2LL *
SegTree[Vertex].add * SegTree[2*Vertex+1].sum;
SegTree[2*Vertex+1].sum += (RightPos - Middle) * SegTree[Vertex].add;
SegTree[Vertex].add = 0;
}
}
void SetValue(int Vertex, int
LeftPos, int RightPos,
int Left, int
Right, int Value)
{
if (Left > Right) return;
if ((LeftPos == Left) && (RightPos == Right))
{
SegTree[Vertex].add = 0;
SegTree[Vertex].set = Value;
SegTree[Vertex].sum = (long long)(Right - Left + 1) * Value;
SegTree[Vertex].sumSq = (long long)(Right - Left + 1) * Value * Value;
return;
}
int Middle = (LeftPos + RightPos) / 2;
Push(Vertex,LeftPos,Middle,RightPos);
SetValue(2*Vertex, LeftPos, Middle, Left, min(Middle,Right), Value);
SetValue(2*Vertex+1, Middle+1, RightPos, max(Left,Middle+1), Right,
Value);
SegTree[Vertex].sum = SegTree[2*Vertex].sum + SegTree[2*Vertex+1].sum;
SegTree[Vertex].sumSq =
SegTree[2*Vertex].sumSq + SegTree[2*Vertex+1].sumSq;
}
void AddValue(int Vertex, int
LeftPos, int RightPos,
int Left, int
Right, int Value)
{
if (Left > Right) return;
if ((LeftPos == Left) && (RightPos == Right))
{
SegTree[Vertex].add += Value;
SegTree[Vertex].sumSq += (long long)(Right - Left + 1) * Value * Value +
2LL * Value *
SegTree[Vertex].sum;
SegTree[Vertex].sum += (long long)(Right - Left + 1) * Value;
return;
}
int Middle = (LeftPos + RightPos) / 2;
Push(Vertex,LeftPos,Middle,RightPos);
AddValue(2*Vertex, LeftPos, Middle, Left, min(Middle,Right), Value);
AddValue(2*Vertex+1, Middle+1, RightPos, max(Left,Middle+1), Right,
Value);
SegTree[Vertex].sum = SegTree[2*Vertex].sum + SegTree[2*Vertex+1].sum;
SegTree[Vertex].sumSq =
SegTree[2*Vertex].sumSq + SegTree[2*Vertex+1].sumSq;
}
long long SumSq(int
Vertex, int LeftPos, int
RightPos, int Left, int
Right)
{
if (Left > Right) return
0;
if ((LeftPos == Left) && (RightPos == Right))
return SegTree[Vertex].sumSq;
int Middle = (LeftPos + RightPos) / 2;
Push(Vertex,LeftPos,Middle,RightPos);
return SumSq(2*Vertex, LeftPos, Middle, Left,
min(Middle,Right)) +
SumSq(2*Vertex+1, Middle+1, RightPos, max(Left,Middle+1), Right);
}
int i, n, q,
cs, tests, type, l, r, x;
int main(void)
{
scanf("%d",&tests);
for(cs = 1; cs <= tests; cs++)
{
scanf("%d %d",&n,&q);
for(i = 1; i <= n; i++)
scanf("%lld",&mas[i]);
build(mas,1,1,n);
printf("Case %d:\n",cs);
while(q--)
{
scanf("%d",&type);
if (type == 0)
{
scanf("%d %d %d",&l,&r,&x);
SetValue(1,1,n,l,r,x);
} else
if (type == 1)
{
scanf("%d %d %d",&l,&r,&x);
AddValue(1,1,n,l,r,x);
} else
{
scanf("%d %d",&l,&r);
printf("%lld\n",SumSq(1,1,n,l,r));
}
}
}
return 0;
}