3986. Истоки и стоки

Вершина ориентированного графа называется истоком, если в неё не входит ни одно ребро, и стоком, если из неё не выходит ни одного ребра.

Ориентированный граф задан матрицей смежности. Найдите все его вершины-истоки и все вершины-стоки.

Вход. Первая строка содержит количество вершин в графе n (1 ≤ n ≤ 100), затем идет матрица смежности – n строк по n чисел, каждое из которых равно 0 или 1.

Выход.  В первой строке выведите количество истоков в графе, затем номера вершин, являющиеся истоками, в порядке возрастания. Во второй строке выведите информацию о стоках в том же формате.

Пример входа	Пример выхода
5 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0	2 3 4 3 1 4 5

РЕШЕНИЕ

графы

Анализ алгоритма

Для каждой вершины i подсчитаем в in[i] количество входящих ребер, в out[i] – количество исходящих. Истоками будут такие вершины v, для которых in[v] = 0 (в которые ничто не входит). Стоками будут такие вершины v, для которых out[v] = 0 (из которых ничто не исходит).

Пример

Граф, приведенный в примере, имеет вид:

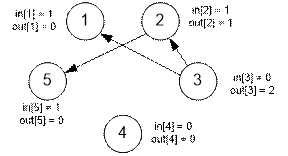
Вершины 3 и 4 являются истоками, так как в них не входит ни одного ребра (in[3] = 0 и in[4] = 0).

Вершины 1, 4 и 5 являются стоками, так как из них не исходит ни одного ребра (out[1] = 0, out[4] = 0 и out[5] = 0).

Реализация алгоритма

Объявим массивы in и out.

#define MAX 110

int in[MAX], out[MAX];

Читаем входные данные. Для каждого ребра (i, j) увеличим на 1 значения out[i] и in[i].

memset(in, 0, sizeof(in));

memset(out, 0, sizeof(out));

scanf("%d", &n);

for (i = 0; i < n; i++)

for (j = 0; j < n; j++)

{

scanf("%d", &val);

if (val == 1)

{

out[i]++; in[j]++;

}

}

Подсчитаем количество истоков source и стоков sink.

source = sink = 0;

for (i = 0; i < n; i++)

{

if (in[i] == 0) source++;

if (out[i] == 0) sink++;

}

Выводим истоки.

printf("%d", source);

for (i = 0; i < n; i++)

if (in[i] == 0) printf(" %d", i + 1);

Выводим стоки.

printf("\n%d", sink);

for (i = 0; i < n; i++)

if (out[i] == 0) printf(" %d", i + 1);

printf("\n");