3986. Sources and sinks
The vertex of directed graph
is called a source if no edge comes
into it, and a sink if no edge comes
out of it.
The directed graph is given
with adjacency matrix. Find all its sources and sinks.
Input. The first line contains the
number of vertices in a graph n (1 ≤
n ≤ 100), then the adjacent
matrix is given – n lines with n numbers, each of them equals to 0 or 1.
Output. Print in the first line the
number of sources in a graph, and then sources in increasing order. Print in
the second line the information about sinks in the same format.
|
Sample input |
Sample output |
|
5 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 |
2 3 4 3 1 4 5 |
SOLUTION
graphs
Algorithm analysis
For each
vertex i, count in in[i] the number of incoming edges, in out[i] count the number of
outgoing edges. The sources will be those vertices v for
which in[v] = 0 (no incoming edges). The
sinks will be those vertices v for which out[v] = 0 (no outgoing edges).
Example
Graph, given in a sample, has the form:
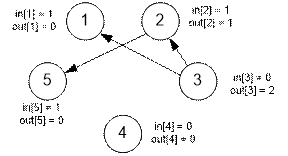
Vertices 3 and 4 are sources, since they have no any incoming edge (in[3] = 0 and in[4] = 0).
Vertices 1, 4 and 5 are sinks, since they have no any outgoing edge (out[1] = 0, out[4] = 0 and out[5] = 0).
Algorithm realization
Declare the arrays in and out.
#define MAX 110
int in[MAX], out[MAX];
Read
the input data. For
each edge (i, j) increase
by 1 the
values of out[i] and in[i].
memset(in, 0, sizeof(in));
memset(out, 0, sizeof(out));
scanf("%d", &n);
for (i = 0; i < n; i++)
for (j = 0; j < n; j++)
{
scanf("%d", &val);
if (val == 1)
{
out[i]++; in[j]++;
}
}
Count
the number of sources and sinks in the variables source and sink.
source = sink = 0;
for (i = 0; i < n; i++)
{
if (in[i] == 0) source++;
if (out[i] == 0) sink++;
}
Print
the sources.
printf("%d", source);
for (i = 0; i < n; i++)
if (in[i] == 0)
printf(" %d", i + 1);
Print
the sinks.
printf("\n%d", sink);
for (i = 0; i < n; i++)
if (out[i] == 0)
printf(" %d", i + 1);
printf("\n");