3987. Полный граф

Неориентированный граф называется полным, если каждая пара его различных вершин соединена хотя бы одним ребром. Для заданного списка рёбер графа проверьте, является ли граф полным.

Вход. Первая строка содержит число вершин n (1 ≤ n ≤ 100) и число рёбер m (1 ≤ m ≤ 10⁴) в графе. Далее следуют m пар чисел, представляющих рёбра графа.

Выход.  Выведите “YES”, если граф полный, и “NO” в противном случае.

Пример входа	Пример выхода
3 3 1 2 1 3 2 3	YES

РЕШЕНИЕ

графы

Анализ алгоритма

Пусть А – матрица смежности. Граф является полным, если во всех ячейках матрицы А кроме диагональных находятся единицы.

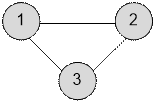
Пример

Граф, приведенный в примере, имеет вид:

Реализация алгоритма

Матрицу смежности графа храним в массиве g.

#define MAX 101

int g[MAX][MAX];

Читаем входные данные. Строим матрицу смежности графа.

scanf("%d %d",&n,&m);

memset(g,0,sizeof(g));

for(i = 0; i < m; i++)

{

scanf("%d %d",&a,&b);

g[a][b] = g[b][a] = 1;

}

Перебираем элементы матрицы, расположенные над главной диагональю. Если все они равны 1, то по окончанию цикла переменная flag будет содержать 1. Если хотя бы один элемент матрицы равен 0, то граф не является полным, flag будет установлен в 0.

flag = 1; // complete graph

for(i = 1; i <= n; i++)

for(j = i + 1; j <= n; j++)

if (g[i][j] == 0) flag = 0;

Выводим ответ.

if (flag == 1) puts("YES");

else puts("NO");

Java реализация

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int m = con.nextInt();

int g[][] = new int[n+1][n+1];

for(int i = 0; i < m; i++)

{

int a = con.nextInt();

int b = con.nextInt();

g[a][b] = g[b][a] = 1;

}

int res = 1;

for(int i = 1; i <= n; i++)

for(int j = i + 1; j <= n; j++)

if (g[i][j] == 0) res = 0;

if (res == 1)

System.out.println("YES");

else

System.out.println("NO");

con.close();

}

}

Python реализация

Читаем количество вершин n и количество рёбер m графа.

n, m = map(int, input().split())

Читаем список смежности. Строим матрицу смежности графа g.

g = [[0] * (n + 1) for _ in range(n + 1)]

for _ in range(m):

a, b = map(int, input().split())

g[a][b] = g[b][a] = 1

Перебираем элементы матрицы, расположенные над главной диагональю. Если все они равны 1, то по окончанию цикла переменная flag будет содержать 1. Если хотя бы один элемент матрицы равен 0, то граф не является полным, flag будет установлен в 0.

flag = 1

for i in range(1, n + 1):

for j in range(i + 1, n + 1):

if g[i][j] == 0: flag = 0

Выводим ответ.

if flag == 1: print("YES")

else: print("NO")