3988. Транзитивность графа

Напомним, что неориентированный граф без петель и кратных рёбер называется транзитивным, если из того, что вершины u и v соединены ребром, вершины v и w соединены ребром и все три вершины u, v и w различны, следует, что вершины u и w соединены ребром.

Проверьте, что заданный неориентированный граф является транзитивным.

Вход. В первой строке заданы количество вершин n и рёбер m графа (3 ≤ n ≤ 100, 0 ≤ m ≤ (n * (n – 1)) / 2). Далее следуют m строк – список рёбер.

Выход.  Выведите “YES” или “NO” – ответ на вопрос о транзитивности графа.

Пример входа 1	Пример выхода 1
3 3 1 2 2 3 1 3	YES
Пример входа 2	Пример выхода 2
3 2 1 2 1 3	NO

РЕШЕНИЕ

транзитивность графа

Анализ алгоритма

Запустим алгоритм транзитивного замыкания графа. Если в графе существуют ребра i → k и k → j, то следует проверить существование ребра i → j.

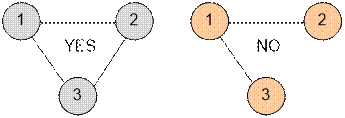
Пример

Графы, приведенные в примерах, имеют вид:

Реализация алгоритма

Матрицу смежности графа храним в массиве g.

#define MAX 101

int g[MAX][MAX];

Читаем входные данные. Строим матрицу смежности графа.

scanf("%d %d", &n, &m);

memset(g, 0, sizeof(g));

for (i = 0; i < m; i++)

{

scanf("%d %d", &a, &b);

g[a][b] = g[b][a] = 1;

}

Запускаем алгоритм Флойда - Уоршела

res = 1;

for (i = 1; i <= n; i++)

for (j = i + 1; j <= n; j++)

for (k = 1; k <= n; k++)

{

if (k == i || k == j) continue;

Если в графе существуют ребра i → k и k → j, то должно существовать ребро i → j.

if (g[i][k] && g[k][j]) res &= g[i][j];

}

Выводим ответ в зависимости от значения переменной res.

if (res == 1) puts("YES");

else puts("NO");