3988. Transitivity of a
graph
Undirected graph
without loops and multiple edges is called transitive, if from conditions
that vertices u and v are connected with an edge, vertices v and w are connected with an edge and all three vertices u, v
and w are different, implies that
vertices u and w are connected with an edge.
Verify that a
given undirected graph is transitive.
Input. The first line contains the number of
vertices n and edges m of the graph (3 ≤ n ≤ 100, 0 ≤ m ≤ (n * (n – 1))
/ 2). Then m lines are given –
the list of edges.
Output. Print “YES” or “NO” – the answer to the
question about transitivity of a graph.
|
Sample
input 1 |
Sample
output 1 |
|
3 3 1 2 2 3 1 3 |
YES |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
3 2 1 2 1 3 |
NO |
SOLUTION
transitivity of a graph
Algorithm analysis
Run the graph transitive closure algorithm. If graph contains edges i → k and k → j, then one should check the existence of
an edge i → j.
Example
Graphs given in samples,
have the form:
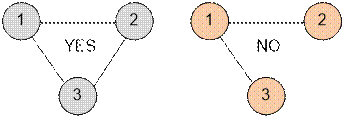
Algorithm realization
Store the
adjacency matrix of the graph in array g.
#define MAX 101
int g[MAX][MAX];
Read the input data. Construct the adjacency matrix of the graph.
scanf("%d %d", &n,
&m);
memset(g, 0, sizeof(g));
for (i = 0; i < m; i++)
{
scanf("%d %d", &a,
&b);
g[a][b]
= g[b][a] = 1;
}
Run the Floyd-Warshall algorithm.
res = 1;
for (i = 1; i <= n; i++)
for (j = i + 1; j <= n; j++)
for (k = 1; k <= n; k++)
{
if (k == i || k == j) continue;
If graph contains edges i → k and k → j, then there
must exist an edge i → j.
if (g[i][k] && g[k][j]) res &= g[i][j];
}
Print the answer depending on the value of res
variable.
if (res == 1) puts("YES");
else puts("NO");