4000. Обход в глубину

Дан неориентированный невзвешенный граф, в котором выделена вершина. Вам необходимо найти количество вершин, лежащих с ней в одной компоненте связности (включая саму вершину).

Вход. В первой строке содержится количество вершин графа n и выделенная вершина s (1 ≤ s ≤ n ≤ 100). В следующих n строках записано по n чисел – матрица смежности графа, в котрой цифра "0" означает отсутствие ребра между вершинами, а цифра "1" – его наличие. Гарантируется, что на главной диагонали матрицы всегда стоят нули.

Выход. Выведите искомое количество вершин.

Пример входа	Пример выхода
5 1 0 1 1 0 0 1 0 1 0 0 1 1 0 0 0 0 0 0 0 1 0 0 0 1 0	3

РЕШЕНИЕ

поиск в глубину

Анализ алгоритма

Запускаем поиск в глубину из заданной вершины s. В счетчике (глобальной переменной) подсчитываем количество вершин, по которым пройдет поиск в глубину.

Пример

Граф, приведенный в примере, имеет вид:

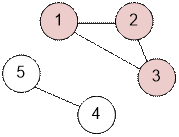
Вершина номер 1 лежит в компоненте связности размера 3.

Реализация алгоритма

Объявим матрицу смежности и массив used использованных вершин.

#define MAX 102

int g[MAX][MAX], used[MAX];

Поиск в глубину из вершины v. В переменной cnt подсчитываем количество пройденных вершин.

void dfs(int v)

{

used[v] = 1;

cnt++;

for (int i = 1; i <= n; i++)

if (g[v][i] && !used[i]) dfs(i);

}

Основная часть программы. Читаем входные данные – матрицу смежности и стартовую вершину s.

scanf("%d %d", &n, &s);

for (i = 1; i <= n; i++)

for (j = 1; j <= n; j++)

scanf("%d", &g[i][j]);

Запускаем поиск в глубину из вершины s.

memset(used, 0, sizeof(used));

cnt = 0;

dfs(s);

Выводим количество вершин, лежащих вместе с s в одной компоненте связности.

printf("%d\n", cnt);