4004. Is there a cycle?

 

The directed graph is given. Determine, does it contain a cycle.

 

Input. First line contains number of vertices n (n ≤ 50). Each of the next n lines contains n numbers, each of them is either 0 or 1. j-th number in the i-th line equals to 1 if and only if there exist an edge from i-th vertex to j-th. It is guaranteed that diagonal of the matrix contains zeros.

 

Output. Print 0 if there is no cycle in the graph and 1 if cycle exists.

 

Sample input 1

Sample output 1

3

0 1 1

0 0 1

0 0 0

0

 

 

Sample input 2

Sample output 2

5

0 1 1 0 0

0 0 0 0 0

0 1 0 1 0

0 0 0 0 1

1 0 0 0 0

1

 

 

SOLUTION

depth first search

 

Algorithm analysis

Start the depth first search on the directed graph as if it was disconnected. In the array used support the colors of the graph vertices:

·        used[v] = 0 – vertex v is white, is not visited;

·        used[v] = 1 – vertex v is gray, we entered vertex v but yet did not proces all its sons;

·        used[v] = 2 – vertex v is black, it and all its sons are processed.

A cycle in the directed graph exists if there is an edge going to a gray vertex in a depth first search.

 

Example

Graphs given in samples, have the form:

 

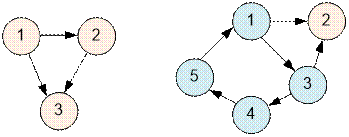
Algorithm realization

Declare an adjacency matrix g and an array of colors used.

 

#define MAX 51

int g[MAX][MAX], used[MAX];

 

Function dfs(v) runs the depth first search from the vertex v.

 

void dfs(int v)

{

 

Vertex v becomes gray, we entered it.

 

  used[v] = 1;

 

Iterate the vertices, where we can go from v.

 

  for (int i = 1; i <= n; i++)

 

From v to i exists an edge if g[v][i] = 1.

 

    if (g[v][i])

    {

 

If vertex i is gray, then during dfs we found a gray vertex, cycle is found.

 

      if (used[i] == 1) flag = 1;

 

If vertex i is white, then we did not visit it yet. Continue search from the vertex i.

 

      else if (used[i] == 0) dfs(i);

 

If vertex i is black, do nothing.

 

    }

 

Vertex v becomes black, exit from it.

 

  used[v] = 2;

}

 

The main part of the program. Read the adjacency matrix.

 

scanf("%d", &n);

for (i = 1; i <= n; i++)

for (j = 1; j <= n; j++)

  scanf("%d", &g[i][j]);

 

Run the depth first search on a directed graph (as on a disconnected one).

 

flag = 0;

for (i = 1; i <= n; i++)

  if (used[i] == 0) dfs(i);

 

Print the answer.

 

printf("%d\n", flag);

 

Java realization

 

import java.util.*;

 

public class Main

{

  static int g[][], used[];

  static int n, flag;

  static void dfs(int v)

  {

    // mark vertex v as GRAY, make an entrance to v

    used[v] = 1;

 

    // we try to go from v to i, i = 1,2,...,n

    for (int i = 1; i <= n; i++)

      // if there exists an edge from v to i

      if (g[v][i] == 1)

      {

         // if vertex i is GRAY, we meet cycle

         if (used[i] == 1) flag = 1;

         // if vertex i is not visited, run dfs from there

         else if (used[i] == 0) dfs(i);

        // if vertex i is black (used[i] = 2), do nothing

      }

    // mark vertex v as BLACK, make an exit from v

    used[v] = 2;

  }

 

  public static void main(String[] args)

  {

    Scanner con = new Scanner(System.in);

    n = con.nextInt();

    g = new int[n+1][n+1];

    used = new int[n+1];

 

    for(int i = 1; i <= n; i++)

    for(int j = 1; j <= n; j++)

      g[i][j] = con.nextInt();

 

    flag = 0;

    // run dfs on directed graph like on disconnected graph

    for (int i = 1; i <= n; i++)

      if (used[i] == 0) dfs(i);

 

    System.out.println(flag);   

  }

}