4008. Биномиальные коэффициенты
Гуннар –
достаточно старый и забывчивый исследователь. Сейчас он пишет статью о
безопасности в социальных сетях, которая включает в себя некоторые элементы
комбинаторики. Он написал программу для вычисления биномиальных коэффициентов,
чтобы проверить некоторые расчеты.
Биномиальный
коэффициент – это число
,
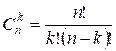где n и k
– неотрицательные числа.
Гуннар
использует свою программу для вычисления 
и получил число m в качестве результата. К несчастью,
поскольку он забывчивый, он забыл числа n
и k, которые он использовал в
качестве входных данных. Эти два числа были результатом долгих вычислений, и
они были записаны на одном из многочисленных листков, лежащих на его столе.
Вместо того чтобы поискать в бумагах, он решил восстановить числа n и k
по полученному ответу. Можете ли Вы помочь ему найти все такие возможные
значения?
Вход. Первая строка содержит количество тестов, не большее 100.
Каждый тест задается в одной строке и содержит целое число m (2 ≤ m ≤ 1015)
– результат программы Гуннара
Выход. Для каждого теста выведите две строки. Первая строка
должна содержать количество способов выразить m при помощи биномиального
коэффициента. Во второй строке должны располагаться все пары (n, k),
удовлетворяющие = m. Пары следует расположить по возрастанию n, а в случае равенства по возрастанию k. Формат вывода пар приведен в примере.
|
Пример
входа |
Пример
выхода |
|
2 2 15 |
1 (2,1) 4 (6,2) (6,4)
(15,1) (15,14) |
РЕШЕНИЕ
комбинаторика
– биномиальные коэффициенты – бинарный поиск
Анализ алгоритма
Если 
= m, то 
= m. Достаточно найти решение k
≤ n / 2 и вместе с парой (k, n)
вывести также пару (k, n – k).
При k = n / 2 эти две пары совпадают.
Пусть p – наименьшее число, для которого 
> m. Тогда очевидно что 0 ≤ k < p.
Зафиксируем
такое k что 
≤ m и рассмотрим функцию f(n) = . Тогда при 2k
≤ n ≤ m функция f(n) является монотонно возрастающей. Следовательно можно решить
уравнение f(n) = m бинарным поиском.
Таким образом
для решения задачи следует перебрать значения k (0 ≤ k < p) и для каждого такого k решить уравнение = m относительно n бинарным
поиском. Найденное значение n должно
быть целочисленным.
Пример
Рассмотрим
уравнение = 3003. Учитывая что 
= 924, а 
= 3432, то нам
достаточно перебрать 0 ≤ k
≤ 6.
Пусть k = 2, рассмотрим уравнение 
= 3003 или 
, n * (n – 1) = 6006. Бинарным поиском в
промежутке 4 ≤ n ≤ 3003
находим целочисленное решение n = 78.
Учитывая что n ≠ 2*k, имеем два решения: 
= 
= 3003.
Реализация алгоритма
Искомые пары
будем хранить в векторе пар res.
vector<pair<long long,long long> >
res;
Функция Cnk вычисляет
значение биномиального коэффициента .
long long
Cnk(long long
n, long long k)
{
long long i, Res = 1;
if (k > n
- k) k = n - k;
for(i = 1; i
<= k; i++)
{
Если на очередной итерации результат превосходит m (мы ищем решение уравнения = m), то останавливаемся. Таким выходом из функции мы также избежим
переполнения.
if (1.0 *
Res * (n - i + 1) / i > m) return m + 1;
Res = Res * (n - i + 1) / i;
}
return Res;
}
Основная часть программы. Читаем входные данные.
scanf("%d",&tests);
while (tests--)
{
res.clear();
scanf("%lld",&m);
Перебираем значение k
от 0 до тех пор пока ≤ m.
for(k = 0;
Cnk(2*k,k) <= m; k++)
{
Ищем значение n (2k ≤ n ≤ m) бинарным
поиском.
long long lo = 2*k, hi = m;
while (lo
< hi)
{
long long n = (lo + hi) / 2;
if
(Cnk(n,k) < m) lo = n + 1; else hi = n;
}
Если 
= m, то решение найдено. Заносим в результат одну или две пары
решений.
if
(Cnk(lo,k) == m)
{
res.push_back(make_pair(lo,k));
if (lo !=
2*k)
res.push_back(make_pair(lo,lo - k));
}
}
Сортируем пары.
sort(res.begin(),res.end());
Выводим ответ – количество найденных пар и сами пары.
printf("%d\n",res.size());
for(i = 0; i
< res.size(); i++)
printf("(%lld,%lld)
", res[i].first,res[i].second);
printf("\n");
}
Python реализация
Функция Cnk вычисляет
значение биномиального коэффициента .
def Cnk(n, k):
Res = 1
if k > n - k:
k = n – k
for i in range(1, k + 1):
Если на очередной итерации результат превосходит m (мы ищем решение уравнения = m), то останавливаемся. Таким выходом из функции мы также избежим
переполнения.
if Res * (n - i + 1) // i > m:
return m + 1
Res = Res * (n - i + 1) // i
return Res
Основная часть программы. Читаем входные данные.
tests = int(input())
for _ in range(tests):
res = []
m
= int(input())
Перебираем значение k
от 0 до тех пор пока ≤ m.
k
= 0
while Cnk(2 * k, k) <= m:
Ищем значение n (2k ≤ n ≤ m) бинарным
поиском.
lo, hi = 2 * k, m
while lo <
hi:
n = (lo + hi) // 2
if Cnk(n, k) < m:
lo = n + 1
else:
hi = n
Если = m, то решение найдено. Заносим в результат одну или две пары
решений.
if Cnk(lo, k) == m:
res.append((lo, k))
if lo != 2 * k:
res.append((lo, lo - k))
k += 1
Сортируем пары.
res.sort()
Выводим ответ – количество найденных пар и сами пары.
print(len(res))
for item in res:
print(f"({item[0]},{item[1]})", end="
")
print()