4018. Черепашка
В левом верхнем углу прямоугольной таблицы
размером n × m находится черепашка. На каждой клетке таблицы разлито
некоторое количество кислоты. Черепашка может перемещаться вправо или вниз, при
этом маршрут черепашки заканчивается в правом нижнем углу таблицы.
Каждый миллилитр кислоты приносит черепашке
некоторое количество урона. Найдите наименьшее возможное значение урона,
которое получит черепашка после прогулки по таблице.
Вход. В первой строке записаны два натуральных
числа n и m, не
превосходящие 1000 – размеры таблицы. Далее идёт n строк, каждая из которых содержит m чисел, разделённых пробелами – описание таблицы с указанием для каждой клетки
содержания кислоты на ней (в миллилитрах).
Выход. Вывести минимальную возможную стоимость
маршрута черепашки.
|
Пример
входа |
Пример
выхода |
|
3 4 5 9 4 3 3 1 6 9 8 6 8 12 |
35 |
РЕШЕНИЕ
динамическое
программирование
Анализ алгоритма
Пусть a[i][j] содержит
количество урона, получаемое черепашкой при посещении клетки (i, j). Пусть dp[i][j] содержит
величину наименьшего урона, которое может получить черепашка при проходе от
клетки (1, 1) к клетке (i, j).
Рассмотрим
базовые случаи:
·
dp[1][1] = a[1][1];
·
dp[i][1] = dp[i – 1][1] + a[i][1], 1 < i ≤ n (первый столбец);
·
dp[1][j] = dp[1][j – 1] + a[1][j], 1 < j ≤ m (первая строка);
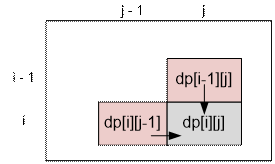
В клетку (i, j) можно попасть
или из клетки (i – 1, j),
или из
клетки (i, j –
1).
Поскольку урон минимизируется, то
dp[i][j] =
min(dp[i – 1][j], dp[i][j – 1]) + a[i][j]
Пример
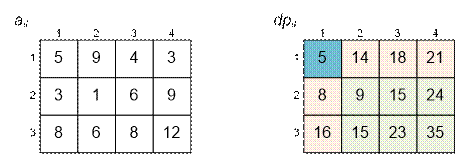
Первый столбец:
·
dp[2][1] = dp[1][1] + a[2][1] = 5 + 3 = 8,
·
dp[3][1] = dp[2][1] + a[3][1] = 8 + 8 = 16.
Первая строка:
·
dp[1][2] = dp[1][1] + a[1][2] = 5 + 9 = 14,
·
dp[1][3] = dp[1][2] + a[1][3] = 14 + 4 = 18.
Вычислим
значения некоторых не приграничных ячеек:
dp[2][2] = min(dp[1][2], dp[2][1]) + a[2][2] = min(14, 8) + 1 = 8 + 1 = 9
dp[3][4] = min(dp[2][4], dp[3][3]) + a[3][4] = min(24, 23) + 12 = 23 + 12 = 35
Искомый путь
черепашки имеет вид:
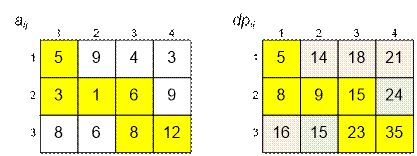
Упражнение
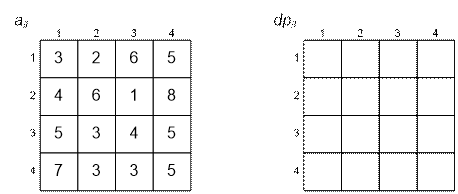
По заданной
матрице a[i][j] заполните
матрицу dp[i][j].
Реализация алгоритма
Объявим рабочие
массивы.
#define MAX 1010
int a[MAX][MAX],
dp[MAX][MAX];
Читаем входные данные.
scanf("%d %d", &n,
&m);
for (i = 1; i <= n; i++)
for (j = 1; j <= m; j++)
scanf("%d",
&a[i][j]);
Инициализация первой строки и первой колонки массива dp.
dp[1][1] = a[1][1];
for (i = 2; i <= n; i++)
dp[i][1] = dp[i - 1][1] +
a[i][1];
for (j = 2; j <= m; j++)
dp[1][j] = dp[1][j - 1] +
a[1][j];
Вычисляем минимальный урон черепашки для каждой клетки.
for (i = 2; i <= n; i++)
for (j = 2; j <= m; j++)
dp[i][j] = min(dp[i -
1][j], dp[i][j - 1]) + a[i][j];
Выводим ответ.
printf("%d\n", dp[n][m]);
Java реализация
import java.util.*;
class Main
{
static int a[][] = new int[1001][1001];
static int dp[][] = new int[1001][1001];
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
a[i][j] = con.nextInt();
dp[1][1] = a[1][1];
for (int i = 2; i <= n; i++)
dp[i][1] = dp[i - 1][1] + a[i][1];
for (int j = 2; j <= m; j++)
dp[1][j] = dp[1][j-1] + a[1][j];
for (int i = 2; i <= n; i++)
for (int j = 2; j <= m; j++)
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + a[i][j];
System.out.println(dp[n][m]);
con.close();
}
}