4019. Черепашка: восстановление

Черепашка хотела бы как можно быстрее пройти по прямоугольной таблице из левого верхнего угла в правый нижний по маршруту с наименьшими потерями.

Вход. В первой строке записаны два натуральных числа n и m (n, m ≤ 1000) – размеры таблицы. Далее идут n строк, каждая из которых содержит m чисел – описание таблицы с указанием для каждой клетки таблицы содержания кислоты на ней (в миллилитрах).

Черепашка может ходить только вправо и вниз в соседние клетки.

Выход. В первой строке выведите одно целое число – минимальный возможный урон для черепашки. В следующих строках выведите координаты клеток, по которым пролегает соответствующий путь. Координаты следует выводить в том порядке, в котором они встречаются на пути.

Пример входа	Пример выхода
3 4 5 9 4 3 3 1 6 9 8 6 8 12	35 1 1 2 1 2 2 3 2 3 3 3 4

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Пусть a[i][j] содержит количество урона, получаемое черепашкой при посещении клетки (i, j). Пусть dp[i][j] содержит величину наименьшего урона, которое может получить черепашка при проходе от клетки (1, 1) к клетке (i, j).

Рассмотрим базовые случаи:

· dp[1][1] = a[1][1];

· dp[i][1] = dp[i – 1][1] + a[i][1], 1 < i ≤ n (первый столбец);

· dp[1][j] = dp[1][j – 1] + a[1][j], 1 < j ≤ m (первая строка);

В клетку (i, j) можно попасть или из клетки (i – 1, j), или из клетки (i, j – 1). Поскольку урон минимизируется, то

dp[i][j] = min(dp[i – 1][j], dp[i][j – 1]) + a[i][j]

Начнем движение из правого нижнего угла (n, m) в левый верхний (1, 1) по пути минимального урона. Инициализируем (i, j) = (n, m). Далее из клетки (i, j) следует двигаться либо в (i – 1, j), либо в (i, j – 1) в зависимости от того какое из этих значений меньше. Если dp[i – 1][j] = dp[i][j – 1], то движение можно продолжать в любую из двух клеток.

Если мы попали в клетку первой строки, то далее двигаемся в угол (1, 1) по клеткам первой строки. Если мы попали в клетку первого столбца, то далее двигаемся в угол (1, 1) по клеткам первого столбца.

Пример

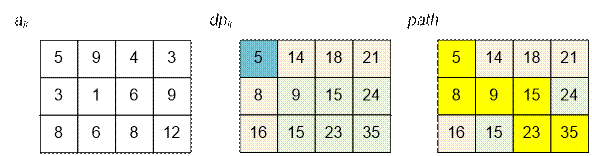
Реализация алгоритма

Объявим рабочие массивы.

#define MAX 1010

int a[MAX][MAX], dp[MAX][MAX];

Читаем входные данные.

scanf("%d %d", &n, &m);

for (i = 1; i <= n; i++)

for (j = 1; j <= m; j++)

scanf("%d", &a[i][j]);

Инициализация первой строки и первой колонки массива dp.

dp[1][1] = a[1][1];

for (i = 2; i <= n; i++)

dp[i][1] = dp[i - 1][1] + a[i][1];

for (j = 2; j <= m; j++)

dp[1][j] = dp[1][j - 1] + a[1][j];

Вычисляем минимальный урон черепашки для каждой клетки.

for (i = 2; i <= n; i++)

for (j = 2; j <= m; j++)

dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + a[i][j];

Выводим минимальный урон, с которым можно достичь правый нижний угол.

printf("%d\n", dp[n][m]);

Инициализируем (i, j) = (n, m). Стартуем движение из правого нижнего угла в левый верхний.

i = n; j = m;

Продолжаем движение пока не достигнем первой строки или первого столбца. Занесем в массив path точку (i, j).

while (i > 1 && j > 1)

{

path.push_back(make_pair(i, j));

if (dp[i - 1][j] + a[i][j] == dp[i][j]) i--; else j--;

}

Двигаемся до точки (1, 1) либо по первой строке, либо по первому столбцу.

while (i > 1) path.push_back(make_pair(i, j)), i--;

while (j > 1) path.push_back(make_pair(i, j)), j--;

path.push_back(make_pair(1, 1));

Путь следует обернуть.

reverse(path.begin(), path.end());

Выводим найденный путь.

for (i = 0; i < path.size(); i++)

printf("%d %d\n", path[i].first, path[i].second);