4021. Ход конём
Дана
прямоугольная доска n × m (n
строк и m столбцов). В левом верхнем
углу находится шахматный конь, которого необходимо переместить в правый нижний
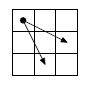
угол доски. В данной задаче конь может перемещаться на две клетки вниз и на
одну клетку вправо или на одну клетку вниз и на две клетки вправо.
Определите,
сколько существует различных маршрутов, ведущих из левого верхнего в правый
нижний угол.
Вход. Два натуральных числа n
и m (1 ≤ n, m ≤ 50).
Выход. Выведите количество способов добраться конём из левого
верхнего до правого нижнего угла доски.
|
Пример
входа 1 |
Пример
выхода 1 |
|
3 2 |
1 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
31 34 |
293930 |
РЕШЕНИЕ
динамическое
программирование
Анализ алгоритма
Пусть dp[i][j]
содержит количество способов, которыми можно добраться из левого верхнего угла
– клетки с координатами (1, 1) в правый нижний угол – клетку с координатами (n, m).
Изначально обнулим массив dp и положим dp[1][1] = 1.
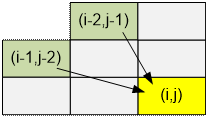
Согласно ходам
коня в клетку (i, j) можно попасть либо из (i – 1, j – 2), либо из (i – 2, j – 1). Следовательно
dp[i][j]
= dp[i – 1][j – 2] + dp[i – 2][j – 1]
Пример
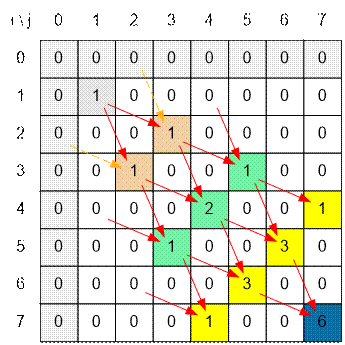
Заполним массив
dp для поля размером 7 * 7:
Реализация алгоритма
Объявим
двумерный массив.
#define MAX 55
int dp[MAX][MAX];
Читаем входные данные.
scanf("%d %d",&n,&m);
Пересчитываем ячейки массива dp. Поскольку в ячейки первой строки и первого столбца конь попасть не
может (кроме начальной
позиции), то циклы по i и по j можно начинать с 2.
memset(dp,0,sizeof(dp));
dp[1][1] = 1;
for (i = 2; i <= n; i++)
for (j = 2; j <= m; j++)
dp[i][j] = dp[i-1][j-2] + dp[i-2][j-1];
Выводим ответ.
printf("%d\n",dp[n][m]);
Java реализация
import java.util.*;
public class Main
{
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
long dp[][]
= new long [n+1][m+1];
dp[1][1]
= 1;
for (int i = 2;
i <= n; i++)
for (int j = 2;
j <= m;j ++)
dp[i][j] = dp[i-1][j-2] +
dp[i-2][j-1];
System.out.println(dp[n][m]);
con.close();
}
}